1 在三维空间中，如果要求沿方向[A,B,C]产生放大到S倍的图形，推导出变换矩阵。A、B和C分别表示直线在x,y和z轴方向的余弦。
(i) 将OP逆时针绕X轴旋转a角，使得OP'落在XOZ面上；
T1 =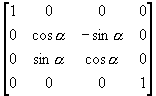 
(ii) 将OP'顺时针绕Y轴旋转b角, 使得OP"与Z轴重合；
T2 =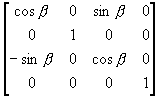 
(iii) 在Z轴上放大
S =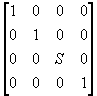 
(iv) 将OP"逆时针绕Y轴旋转b角
=
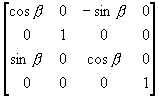
(v) 将OP顺时针绕X轴旋转a角
=
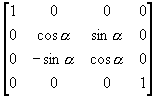
cosα =
sinα= 
cosβ = 
sinβ
= A
M =
S T2 T1
2 (a) 写出通过点（0，0，0）和（1，2，3）的直线参量方程；
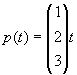
(b) 写出通过点（1，2，3），（－1，2，3）和（1，2，－3）的平面方程；
y - 2 = 0;
(c) 写出通过点（1，2，3）而且垂直于矢量（4，2，3）的平面方程；
4x + 2y +3z -17 = 0;
(d) 写出由（a）描述的直线和(b)描述的平面的交点。
3 对于下列变换写出它们的齐次坐标变换矩阵
(a) 将x和y放大为原来的三倍，且图形点（0.5，0.2，－0.2）保持不动；
T1 =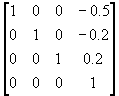 
S
=
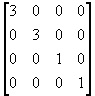T1 =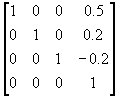 
T = T2 S T1 =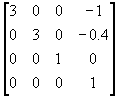 
(b) 绕过点（0，0，1）和点（－1，－1，－1）的直线旋转π/4；
(i) 平移点（0，0，1）到原点
T1 = 
(ii) 将直线绕X轴逆时针旋转α角度
T2 =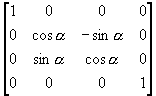
cosα = 2 
/5,
sinα =
/5
(iii) 将直线绕Y轴顺时针旋转β角度
T3 =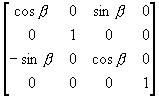 
cosβ = 
/6,
sinβ = 
/6
(iv) 将直线绕Z轴逆时针旋转p/4
T4 =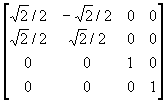 
(v) 将直线绕Y轴逆时针旋转β角度
T5 =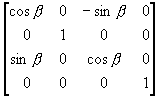 
(vi) 将直线绕X轴顺时针旋转α角度
T6 =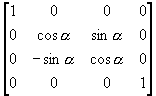 
(vii)
T7 =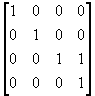 
M = T7T6T5T4T3T2T1
(c) 产生对原点对称的图形；
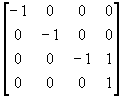
(d) 产生对ｚ＝3平面对称的图形。
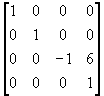
4 在右手坐标系中从原点到P（x,y,z）的直线，用下面三种次序都可以将此直线旋转到正的ｚ轴上。求出变换矩阵。这三个组合变换阵是否相同？
(a) 绕x轴旋转到x-z平面上，再绕y轴旋转到z轴上；
(i) 绕x轴旋转到x-z平面
T1 =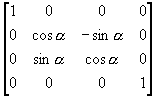 
(ii) 再绕y轴旋转到z轴
T2 =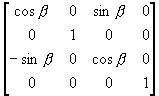 
M = T2 T1 =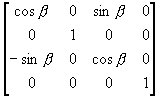 
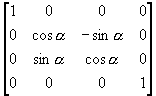
(b) 绕y轴旋转到y-z平面上，再绕x轴旋转到z轴上；
(i) 绕y轴旋转到y-z平面上
T1 =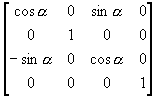 
(ii) 再绕x轴旋转到z轴上
T2 =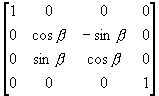 
(c) 绕z轴旋转到x-z平面上，再绕y轴旋转到z轴上。
(i) 绕z轴旋转到x-z平面上
T1 =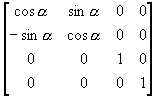 
(ii) 再绕y轴旋转到z轴上
T2 =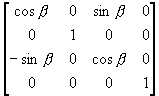 
cosα =a /
sinα = b /
cosβ =
, sinβ = c;
5 设M是三维坐标变换，若已知空间四点的变换关系A·M＝A'，B·M＝B'，C·M＝C'和D·M＝D'，如何求出该变换M？若M-1是M的逆变换阵，而N是三种基本几何变换阵的一种，是否能不用对M·N直接求逆阵而求得[M·N]-1
联立，求解方程组。