|
6.3.3 产生与测试方法
产生与测试方法是一种模型驱动方法。尽管它只用很简单的模型，该方法也显示出模型驱动方法的特点：抗干扰性好，不能逐步接受新例子并修改概念。下面介绍INDUCE1.2算法(Dietterich和Michalski,1981)。
1． INDUCE 1.2
它只由示教正例学习单个概念。这是在规则空间中寻找少数概念，使每个概念都覆盖全部示教例子。这类似于消除候选元素算法修改S集合。程序把示教例子转换成规则空间中的点，即例子和规则使用统一的表示形式。选择示教例子，使其对应的点形成规则空间中向上的放射搜索。这就是由特殊的例子到一般的概念。一般化的方法是去掉合取条件或增加析取选择。放射搜索的过程是：
第一步：使集合H初始化为包含示教例子中任一个大小为W的子集，W称放射宽度。
第二步：产生更一般化的概念。以各种方式去掉单个条件，以便使H中每个概念一般化。这形成了新的H。
第三步：修剪H中可能不合理的概念，使H中只保留W个概念。修剪的一个准则是根据概念描述的句法特性，如项的数目和用户定义项的代价。另一个准则是使H中每个元素覆盖最多的例子。
第四步：测试H。检查H中每个概念是否覆盖全部示教例子。如果某个概念是这样，就从H中去掉，并放入输出概念的集合C中。
第五步：重复二、三、四步，直到C达到予定大小或H为空。
INDUCE 1.2的放射搜索示意图如 图 6.9所示。
 |
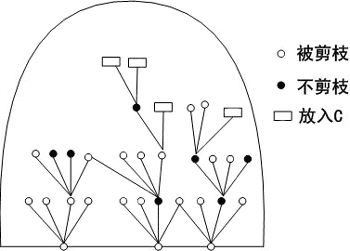 图6.9 放射搜索 |
2． 算法的推广
第一类推广是用于学习二元谓词或高阶谓词表示的概念。例如表示两个积木接触的谓词TOUCH(a,b)就是二元谓词。有些问题虽然也可以用一元谓词或函数表示，但不如用二元谓词表示时简单、自然。
第二类推广是提高搜索规则空间的效率。Dietterich 和Michalski 使用了两种不同的规则空间。第一种规则空间是只描述结构的空间，它是只用二元或多元谓词表示的概念的空间。示教例子投影到这个空间(去掉一元谓词和函数)，然后在此空间进行放射搜索。一旦在这个空间得到概念集合C，就用C中的每个概念定义第二种规则空间。对C中的概念Ci,第二种空间中的概念中只需用Ci中的子对象的特征来表示。于是就可以用特征向量表示该空间。再把示教子换成该空间中的点，进行放射搜索，找到概念集合C'。把C'中的概念与Ci组合，就构成一个完整的概念。
例如考虑下列两个正例。
 |
例1 |
| LARGE (u)∧CIRCLE(u)∧LARGE(v)∧CIRCLE(v)∧ONTOP(u,v) | |
|
例2 |
| SMALL(w)∧CIRCLE (w)∧LARGE(x)∧SQUARE (x) ∧LARGE(y)∧SQUARE(y)∧ONTOP(w,x)∧ONTOP (x,y) |
例1表示大圆u在大圆v上方。例2表示小圆w大方x上方，且x在大方y上方。把两个例子投影到只描述结构的规则空间，就得到下列示教例子。
|
例1' |
| ONTOP(u,v) | |
|
例2' |
| ONTOP(w,x)∧ONTOP(x,y) |
在这个空间的放射搜索发现，描述结构的唯一概念是C={ ONTOP(u,v)}。它符合示教例子。
然后由特征u和v 发展出新规则空间。描述这个空间的特征向量是
(SIZE(u),SHAPE(u),SIZE(v),SHAPE(v))
把示教例子例1和例2变换到这个空间就得到新的例子。
|
例1" |
| ( large, circle, large, circle ) | |
|
例2.1" |
| ( small, circle, large, square ) | |
|
例2.2" |
| ( large, square, large, square ) |
注意，由例2'得到了两个例子(例2.1"和例2.2")，因为例1'可以用两种方式匹配例2'。一种是u约束到w,v约束到x；另一种是u 约束到x,v约束到y。在第二种空间的放射搜索产生两个覆盖全部例子的概念
( large, *, large, * )
和( *, circle, large, * )。
这是进行尽量减少一般化的结果，其中的*表示该特征值无关，这两个概念构成C'。把他们与C中的概念组合，就得到两个完整的概念。
：ONTOP(u,
v)∧LARGE(u)∧LARGE(v)
：ONTOP(u,v
)∧CIRCLE(u)∧LARGE(v)3. INDUCE1.2 优缺点
它的优点首先是比变型空间方法更快，存储量更少，其次是它有良好的抗干扰性。如果提供有干扰的示教例子，就要修改过程第四步。应使选中的概念覆盖大多数例子，不必覆盖全部例子。
它的缺点首先是缺乏强有力的模型去指导修剪和结束搜索。它的修剪准则比较弱。应该考虑用论域知识改进修剪。其次是在第二步全部罗列H中假设的所有单步一般化。在大的规则空间中，这样作代价太大。改进方法是只产生可能合理的假设。第三是它进行了修剪，所以是不完备的。它不一定能找到全部合格的概念。第四是要求同时提供全部例子，不适于逐步学习。