Stephenson可测性分析将可控性和可观性都定义为0到1之间的值。 　　对可控性(CY )来说，外部输入端的可控性最强，令CY=1。完全不可控的节点其CY=0。电路内部一般节点的可控性的值在0～1之间。 　　对可观性(OY )来说，外部输出端的可观性最强，令OY=1。完全不可观的节点其OY=0。电路内部一般节点的可观性的值在0～1之间。可观性是相对于某一观察点而言的。同一个节点，相对不同的观察点，其可观性的值不同。 　　这里定义的可控性和客观性比较好地反映了实际情况。也比较容易理解。还有其它的定义方法，不再赘述。 　　一个逻辑单元输出端的可控性定义如下： 　　　CYout = CTF·f ( CYIn ) 　　其中，CTF为可控性传递因子，f (CYIn )是对该输出有控制作用的各输入的组合函数。 　　已知外部输入端可控性为1，利用CTF可以从外部输入端开始一个一个元件依次计算其输出端的可控性，直到求出所有的元件输出端的可控性。可观性的求法类似。注意不是输出端的可控性最小，而是中间的不可控节点的可控性最小，设为0。 　　CTF描述了输出状态由'0'转换到'1'或由'1'转换到'0'的难易程度，它只取决于逻辑单元的逻辑函数，与该单元在电路中的位置无关，即与逻辑单元输入端的可控性无关。 　　　 　　式中N(0)和N(1)分别表示使输出取值为'0'和'1'的方法数。对于一个n输入端的逻辑单元，由于每个输入端可以取'0'和'1'两种值，故有 　　　N(0) +N(1)=2n 　　例如一个二输入端与门，使输出为'0'的方法有1种，使输出为'1'的方法有3种，故 　　　N(0)=1, N(1)=3 　　因而 　　　 　　基本逻辑元件的CTF是固定的。可以预先求出，使用时查表即可。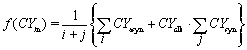 　　对于一般的逻辑单元，f(CYIn )为人为定义的逻辑单元输入端的平均可控性与每个输入端（前级输出端）可控性的关系，可定义为 　　　 　　其中CYasyn表示各异步输入端的可控性，CYclk表示时钟输入端的可控性，CYsyn表示各同步输入端的可控性。对于一个组合电路单元，上式可表为 　　　 　　即各输入端可控性的平均值。i为输入端个数。 　　对于一般的逻辑单元，各输入端的贡献可能不一样，上面的公式给出求整个逻辑单元平均可控性的方法。