与普通组合电路相比, 迭代组合电路有下列特点:
(1)迭代组合电路是一个组合电路模块的多次重复。每个组合电路模块称为一帧。各个帧有完全相同的结构, 仅仅在对应点上信号值不同。由对应点上的信号值组成的空间序列, 恰好是原时序电路关于时间的序列。因此, 在处理迭代组合电路时并不需要真正构造一个这样的电路, 只需存储基本组合电路模块的连接信息, 每一个节点的信号值以向量形式(即时间序列)存储。
(2)迭代组合电路的测试输入向量和输出向量均以序列形式出现, 实际表示原电路的时间序列。
(3)迭代组合电路除了输入向量和输出向量之外, 还必须考虑其内部状态向量。为了保证所求得的测试在任意初始内部状态下均可适用, 通常要求初始状态均为'X',即要求在反向一致性操作中,最终达到内部状态变量的值均为'X'。
(4)原电路的单故障在展开的迭代组合电路的每帧中出现, 形成多故障问题。
在利用D算法求迭代组合电路的测试时, 必须考虑这些特殊问题进行特殊处理, 从而形成了扩展D算法。
扩展D算法以一个基本的帧为出发点, 按一般D算法进行, 力求把故障D 或D 传播到输出端, 如果在本帧不能传播到输出端, 则向后进行迭代, 即在后面增加一帧继续传播。如此迭代直到在某一帧的输出端得到D 或D 。我们用p来记录向后迭代时新增加的帧数。
当D 或D 被驱赶到输出端后, 进行一致性操作。一致性操作要保证有确定的输入向量, 并且要求其初始内部状态均为'X'。如果不能做到这一点, 则向前进行迭代, 即在前面增加一帧继续进行一致性操作。如此反复操作直到达到一致性操作目的为止。我们用q来记录向前迭代时新增加的帧的个数。
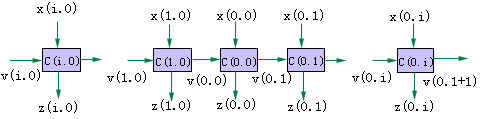
设p和q 的初始值均为0, 经过成功迭代运用D算法之后得到如图7.17所示的电路。其中最后一帧C(0, i )的输出Z(0, i)得到了D 或D , 最前一帧C(j, 0)的内部状态y(j, 0)各值均为'X'。各模块的输入量x(j, 0),…, x(0, 0),…, x(0, i)组成测试输入序列。这里x, y, z的第一个下标表示q, 第二个下标表示p。
|
图7.17 扩展D算法结果
|