(3)正常情况下的值a = 1, g = 1。这时，a的值与故障值相同，而g的值与其故障值不同。先不考虑a，只要考虑关于g的一阶布尔差分，即其测试向量应满足
　　　　
而
　　　　
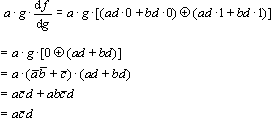
所以其测试向量为(a, b, c, d) = (1, X, 0, 1)。
　　综合上述三种情况，故障as-a-1 , gs-a-0的测试向量的集合为
　　　　
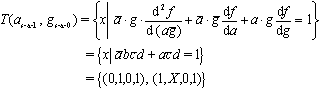
　　这里求得的测试向量的集合是所有可能的测试向量的全集，即(0, 1, 0, 1), (1, 0, 0, 1), (1, 1, 0, 1)。实际上只要其中的一个向量就可以检测出这两个故障。其中的(1, 1, 0, 1)与前面用D算法求出的结果相同。
　　一般情况下，二阶布尔差分可以定义为
　　　　
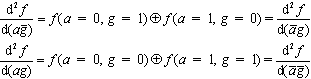
因而，对于a, g的各种故障的组合，可以得到求测试集公式：
　　　　
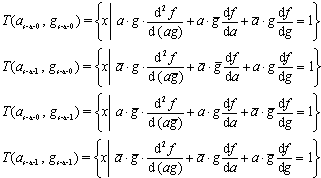
　　高阶差分可以类推，并可得到多故障电路的测试向量全集。例如求三个故障的测试集全集公式为
　　
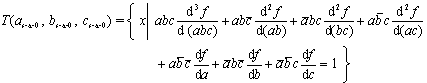
　　二阶布尔差分的实质与二故障D算法的基本概念相同，都有几种故障点正常值组合。一般来说，多故障的布尔差分要比原函数简单，差分的阶越高，表达式就越简单。但公式看起来要复杂一些。读者只要找到规律，就不难写出这些公式。