(1)正常情况下的值a = 0, g = 1，分别将正常值和故障值代入布尔函数f (a,b,c,d,g )中，得
　　　　f (a = 0, g = 1) = 0·d·1+b·d·1 = b·d
　　　　f (a = 1, g = 0) = 1·d·0+b·d·0 = 0
测试输入应满足
　　　　f (a = 0, g = 1)f (a = 1, g = 0)＝b·d0 = b·d
　　　　a = 0,
　　　　g=a·b+c
即要求：
　　　　a·g·[f(a = 0,g = 1)f(a = 1,g = 0)] =a·(ab+c)·bd = abcd = 1
而得到测试向量为(a, b, c, d) = (0, 1, 0, 1)。
　　类似于单故障情况，我们把f(a = 0, g = 1)f (a = 1, g = 0)定义为二阶布尔差分：
　　　　 = f(a = 0, g = 1)f (a = 1, g = 0)
这样，上述测试输入的条件可以描述为
　　　　
　　(2)正常情况下的值a = 0, g = 0。这时，a的值与故障值不同，而g的值与其故障值相同。先不考虑g，只要考虑关于a的一阶布尔差分，即其测试向量应满足
　　　　
而
　　　　
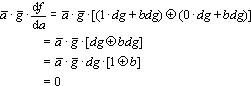
所以这种情况下没有测试向量。