图7.10 D算法举例电路

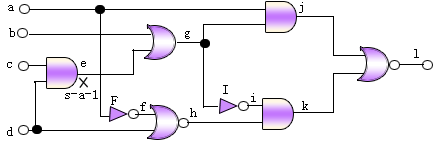　　先求故障e_s-a-1的故障原始D立方pdcf，以及各元件的质覆盖cover和传播D立方pdc。
　　　　pdcf (e_s-a-1) =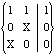∩_pdcf{ X X|1 }=
　　　　cover(AND2) = 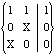, pdc(AND2) =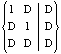
　　　　cover(OR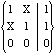2) = , pdc(OR2) =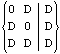
　　　　cover(NOR2) = 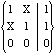, pdc(NOR2) =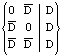
　　　　cover(NOT) = , pdc(NOT) = { D | D }
　　参看表7.9的D算法执行过程。
　　1． 开始，将故障e_s-a-1的一个故障D立方{0 X | D}作为初始测试D立方tc₀ 。其D前沿为{G}，C前沿为空。
　　2． 做D驱赶，用G的传播D立方{0 D| D}与tc₀作D交，得tc₁。g的负载元件有J和I，作为新的D前沿，C前沿仍为空。
　　3． 选J做D驱赶，用J的传播D立方{1 D| D}与tc₁作D交，得tc₂。又得新的D前沿元素L，放入D前沿DF中。C前沿为空。
　　4． 选L做D驱赶，得tc₃。D到达了输出端。但C前沿中有K，需要做一致性操作。
　　5． 选K的一个质立方与tc₃作D交，得tc₄。这时D前沿中又有元素I，再做一致性操作。
　　6． 选I的质立方{ 1| 0 }与tc₄作D交，结果为空。
　　7． 回溯到tc₃，选K的另一个质立方再做一致性操作，得tc₆。
　　8． 这时C前沿中又出现新元素H，再做一致性操作，得tc₇。
　　9． 这时C前沿为空，所有信号的值已确定，输出端也出现了D。D算法获得成功。于是得到故障e_s-a-1的一个测试向量T = { 1 0 0 1 }。