·传播D立方(Propagation D-Cube, 简记为pdc):又称为原始D立方(Primitive D-Cube)。它描述一个元件对D或D传播的特性。其特点是元件的输入和输出两方均必须有D或D出现。输入方有两个以上的D或D称为多重传播D立方。
传播D立方的目的是把该元件某个或某几个输入端的D值(D或D)传播到输出端,使输出端也存在D或D。
传播D立方可以由元件的质覆盖求得。设元件的质覆盖为G,其中输出部分为0的质立方集合为g0,输出部分为1的质立方集合为g1。将二者作pdc交运算。pdc交运算规则如表7.7所示:(输入和输出部分规则相同)
|
表7.7 输入/出部分的pdc交运算
|
| 0 | 1 | X | |
| 0 | 0 | D | 0 |
| 1 | D | 1 | 1 |
| X | 0 | 1 | X |
例如与非门的g1为{ 0 X | 1, X 0 | 1}, g0为{1
1 | 0 }。由g1与g0作pdc交运算。得{ 1 | D, 1 | D }。由g0与g1作pdc交运算。得{
D 1 | , 1 D | }。
它意味着,若有一个输入端为1时,另一个输入端的D或D可以传播到输出端,分别为D或D。
不难看出,由于两种结果只是把两个立方体顺序颠倒,因此求出来的结果具有对称性,我们称它们为互补。实际计算时,只要把一种结果的所有D改为D,D改为D即可得到其互补传播D立方。
互补也称为对偶。
为了求多重传播D立方,需要首先对元件质覆盖中的各个多维立方两两相交,得到立方体的各个面,再进行上述pdc交运算。例如与非门的例子,
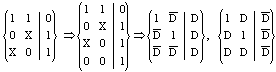
对于3输入端与非门,
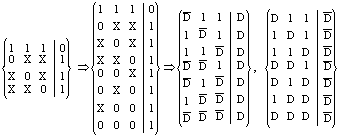
只有在需要时才求多重传播D立方。