·记号D和D：一个电路存在故障时，某些信号值与正常状态下的值不同。当正常状态下的值为'1'，而存在故障时的值为'0', 就用D来表示。反之，若正常状态下的值为'0'，而存在故障时的值为'1', 就用D来表示。对于故障点，则可以用D表示故障s-a-0，用D表示故障s-a-1。
电路中各节点的逻辑值除了0，1，X外，又加了D和D，共5个值。
·故障原始D立方(Primitive D-Cube of Fault，简称pdcf)：表示故障点作为输出端的元件，当输出端为D或D时的输入端向量组成的立方体集合。
通常对故障点为其输出的元件（下面称故障元件）求pdcf。Pdcf表明故障元件输入和输出之间的关系。如果故障点是外部输入，则可直接把该点的D值（D或D）作为pdcf。
求pdcf的方法是：将无故障元件的覆盖G与其有故障元件的覆盖B作一特殊的pdcf交运算。其规则为：
(1) 输入部分的pdcf交运算与一般立方体交运算相同；
(2) 输出部分的pdcf交运算规则如表7.6所示:
|
表7.6 输出部分的pdcf交运算
|
| G的输出部分取值 | 1 0 0 1 |
| B的输出部分取值 | 0 1 0 1 |
| pdcf的输出部分取值 | D D  |
(3)步骤(1)和(2)中若出现则故障原始D立方pdcf为空(φ)。
例1 设一个与门输出端有故障s-a-1。则无故障覆盖G和有故障覆盖B分别为
，B={
X X | 1 }--b1
因为g1和b1，g0和b0其输出部分的pdcf交运算结果分别为，实际上不用求。只要把g1与b0，g0与b1分别进行pdcf交运算即可。前者得到输出为D的故障D立方，后者得到输出为D的故障D立方。此例不存在b0，只需要对g0与b1进行pdcf交运算：
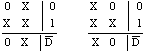
因此故障s-a-1的pdcf为
例2 设一个与门在故障状态下表现为或门性质，求其pdcf。
正常状态下的覆盖G和故障状态下的覆盖B分别为
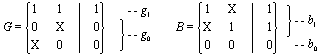
首先对g1与b0进行pdcf交运算，
结果为空。
下面对g0与b1进行pdcf交运算：
得该与门的pdcf为
注意必须是无故障立方体与有故障立方体相交，不能反过来，其结果会不同。以上讲的方法是一般性的方法。通常单固定故障情况下，单输出故障元件的输出端有故障，输入端无故障，因而有故障时的立方体输入部分都是X，即（XX..X|1）或（XX..X|0）。因而这种情况下，只要将立方体中输出值与故障值不同的立方体找出来，将输出部分的1改为D(故障值为0),
0改为D(故障值为1)。