单路径敏化法方法简单,缺点是不能保证对任一非冗余故障都能找到测试向量。典型的情况是故障处于再会聚路径(Reconvergent Path)中。图7.8所示的电路中,信号节点f经过门I,J又会聚到m,就是典型的再会聚路径结构。设节点f有故障s-a-0。f的无故障值'1'要求外部输入端a、d的值均为'1'。按照单路径敏化法,当我们选择路径f-i-m时,节点b, h, j, k必须同时为'1'。节点j为'1'要求c为'0',以保证不管节点f有没有故障都使节点j为'1'。而c为'0'必然使g的值为'1'。要使k为'1', 必须使g和d的值至少有一个为'0',这与g和d的值均必须为'1'相矛盾,因而该路径的敏化失败。从f到m还有一条路径f-j-m,这条路径与前一条路径结构对称,同样不能找到测试向量。可见,用单路径敏化法找不到故障fs-a-0的测试向量。而测试向量确实存在。实际上只要同时使两条路径敏化,就能解决问题。也就是说,必须用多路径敏化法。下一节介绍的D算法就是多路径敏化法,可以找到故障fs-a-0的测试向量。
图7.8 再汇聚路径结构的电路 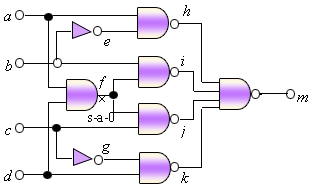 |
用一种算法找不到测试不等于不存在测试,这时我们说算法失败,而不说没有测试。上面的例子中单路径敏化法就找不到测试,而用D算法能找到测试。