OBDD的大小和形状不但与函数本身有关,也依赖于变量的顺序。对于同一函数,好的变量序的选择可以大大简化它的OBDD表示。图6.4布尔函数a1b1+a2b2+a3b3不同变量序的OBDD表示,图中(a)图变量序为a1<b1<a2<b2<a3<b3,(b)图变量序为a1<a2<a3<b1<b2<b3,仅仅由于变量序的不同,左图的非叶子节点数等于输入变量数,而右图的非叶子节点数则与输入变量数成指数关系。表6.1中给出几个通用布尔函数OBDD表示的复杂性。从表中可看出,有些函数可以通过选择一个好的变量序来简化,而对另一些函数,例如整数的乘法,不论怎样选择变量序,它的OBDD表示总是与输入变量数成指数关系。在实际应用中,变量序的选择一般是通过启发式算法来进行。只要能避开指数级增长,OBDD这种表示方法就能有相当高的效率。
图6.4一个布尔函数的不同变量序的OBDD表示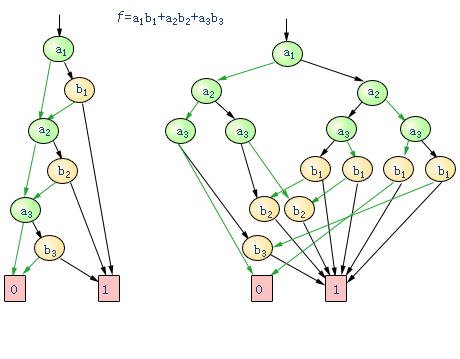 |
表6.1 几种常用函数的OBDD的复杂性
| 函数类型 | OBDD复杂性 | |
| 最好的变量序 | 最好的变量序 | |
| 对称函数 | 线性 | 二次方 |
| 整数加法 | 线性 | 指数级 |
| 整数乘法 | 指数级 | 指数级 |
由此可见,寻找变量序是非常关键的一件事情,这方面有不少的研究成果,典型的方法是根据电路图结构各输入变量对电路内部节点和输出的影响来决定变量序。因篇幅关系,本书不再详细讨论。