下面给出BDD化简的三条规则，经过下述规则化简后的BDD与原BDD在功能上等价。 　　　删除重复的叶子节点：对于一个给定的标号，删除所有重复的叶子节点，只留下其中一个，并把指向已删除叶子节点的弧指向保留的那个叶子节点。 　　　删除重复的非叶子节点：对于非叶子节点u和v，如果var(u)=var(v)，lo(u)=lo(v)，hi(u)=hi(v)，删除两个节点中的一个，并把指向已删除节点的弧指向未删除的那个节点。 　　　删除冗余非叶子节点：对于非叶子节点u，如果lo(u)=hi(u)，删除u节点，并把指向u节点的弧指向lo(u)。 　　从任何一个有序二叉判决图OBDD开始，我们可以不停地应用上述规则对之进行化简。我们称最大程度化简了的有序BDD为ROBDD。下面我们提到OBDD就是指ROBDD。 　　图6.3给出将图6.2所表示的有序BDD化简至OBBD的过程。A中应用第一条规则将八个叶子节点减少到两个，B中应用第二条规则将四个非叶子节点x3减少到两个，C中应用第三条规则删除两个非叶子节点。一般来说，这三条规则要反复使用，因为每次应用其中一条规则进行化简所产生新的BDD都可能需要应用其它规则做进一步化简。　　 图6.3 有序BDD的化简为ROBDD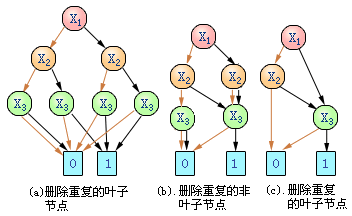 　　OBDD有一个非常重要的性质：用OBDD表示布尔函数是正则的，即对于给定的一个变量序，一个布尔函数的两个OBDD是同构的。 　　这个性质有几个重要结论，可以很容易判断函数的等价性。一个布尔函数是可满足的当且仅当它的OBDD表示不能归结为只有一个标号为0的叶子节点。重言式的OBDD表示一定有标号为1的叶子节点。如果一个布尔函数与变量x无关，则这个函数的OBDD表示中一定不含有标号为x的节点。因而，一个布尔函数的OBDD表示建立了，它的许多函数性质就可以很容易地被检测。