用二叉判决图BDD来表示布尔函数是Akers^[6]在1978年提出的。1986年，Randal E. Bryant对BDD进行改进^[7]，对BDD中的变量顺序作了一些限制，从而使BDD成为一种正则的布尔函数表示方法。
　　BDD是基于先农多项式(Shannon expansion)展开得到的，对f(x₁,…, x_n)来说，先农多项式为：
　　
　　BDD用图来表示，是一个带根的有向无环图。图6.2给出函数f(x)=x1x3+x2x3 的真值表和BDD表示。从图中可看出，在未经化简的情况下，BDD为完全二叉树。每一个非叶子节点v被标上变量var(v)，并有弧指向两个孩子：lo(v)（用虚线表示）代表该变量取值为0，hi(v)（用实线表示）代表该变量取值为1。叶子节点被标为0或1。对于给定的一组变量值，从根节点到叶子节点的一条路径是确定的，函数的值也就是该叶子节点的值。由于给定了变量序和分解顺序，该BDD中叶子节点的值（从左到右）与真值表中的值（从上到下）一一对应。

图6.2 函数f(x)=x1x3+x2x3 的真值表和BDD表示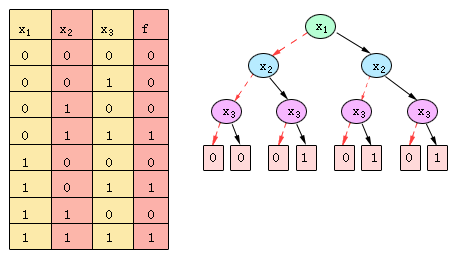

　　BDD是布尔函数的一种表示方法，从图中我们可以看到，它的每条指向叶子节点的路径都是一个真值表项。因此，BDD只是确定了电路的功能，而未确定电路的结构。
　　对于BDD，我们对所有变量进行排序，规定对于任一顶点u和它的非叶子节点v，它们所代表的变量的顺序为var(u)<var(v)，这样得到的BDD成为有序BDD(Ordered BDD), 简称为OBDD。例如，在图6.2的BDD中，变量序为x₁<x₂<x₃。从理论上讲，变量序可任选，但在实际上，变量序对BDD的化简起着十分重要的影响，不同的变量序经过化简过程所得到的BDD有很大的不同。在进行BDD的运算和操作时，一个好的变量序的选择可以节省大量的时间和空间。
　　如果不化简，各种变量序的BDD都是完全二叉树，其节点数也相同，都是对变量指数级的，其叶子节点数为2ⁿ个。这样的表示法是无法使用的，而化简后的BDD则在节点数量上大大减少，从而获得应用。