图6.1 判断 两个FSM等价的异或模型电路A B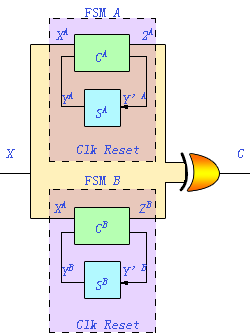

　　图6.1示意两个同步有限状态机A和B的等价性判断。令C^A和C^B分别表示A和B的组合电路部分，而S^A和S^B分别表示A和B的状态寄存器集合。设x={x₁, ... , x_n }为输入集合，z={z₁, ... ,z_m}为输出集合， y={y₁, ... ,y_k }为当前状态变量集合， y'={y'₁, ... , y'_k }为下一状态变量集合，X[t], Z[t], Y[t]和Y'[t]分别表示在时钟周期t的输入、输出、当前状态变量和下一状态变量的值向量。为了对A和B进行功能比较，建立一个异或模型电路A × B，用输入向量x同时施加于A和B，其相应的输出向量z^A和z^B通过XOR函数逐对进行比较，其结果形成信号c。两个电路A和B功能等价，当且仅当SA和SB的初始状态为相同的状态Y^A[0]= Y^B[0]，输入序列(X[0], ... , X[t])始终产生一个常量值c=0。
　　读者可以根据时序电路等价的示意图（图6.2）画出组合电路等价的示意图。基本思路是对任意输入向量其输出向量应该是相同的，即其异或结果应为0。对于定理证明来说，只要有一个向量能使得两个电路输出不同，即异或运算为1，则说明这两个电路不等价。这就是所谓的反证法。
　　常用的时序电路的逻辑验证方法也有两种。
　　(1)定理证明技术。运用公理和已经证明的定理证明电路的描述是正确的。这种方法可以表示几乎所有的行为系统特性。但这种方法需要大量的用户知识，需要用户对证明过程的引导，以便成功地验证实际的设计。理论证明的方法一般基于数理逻辑体系。如命题逻辑、一阶逻辑、高阶逻辑及时态逻辑等。
　　与通常的定理证明相类似，形式验证常用的方法有：形式推理法，反证法和归纳断言法。形式推理法由电路描述出发，根据公理和定理作等价变换和推理，推出设计要求的描述。而反证法则是首先对设计要求的描述作否定假设，再寻找可以产生这个否定假设的条件。如果存在这样的条件，表示描述不正确；如果不存在这样的条件，则验证成功。一般情况下，常常要求用户指定逻辑电路所要实现的功能，称为断言(Assertion)，验证的任务是证明这个断言为真。断言的指定，通常用谓词和逻辑关系式表示电路中某一点与输入变量之间的关系。 VHDL语言规定了断言指定方法(Assert语句)。归纳断言法则对各种初始条件证明断言为真。
　　(2)状态搜索技术。通过自底向上地显式或隐式访问模型电路A × B的所有可到达状态，判断对从初始状态出发的各个路径的状态转换结果都使A × B的输出结果c为常数'0'，　从而证明A与B等价。引入BDD表示状态集合，用深度优先的或广度优先的方法搜索FSM图，使得这种方法可以用来验证具有大量状态的硬件设计。状态搜索技术比理论证明容易用计算机实现。因而可用于验证实际的硬件设计。然而，表示实际电路状态集的BDD的规模也常随状态个数指数增加，限制了其通用性。
　　如果两个FSM具有相同的状态编码，在状态位y={y₁, ... ,y_k }到 y'={y'₁, ... , y'_k }之间一一对应，时序验证的任务变得更容易。证明过程为如下三个步骤：
　　　　Y^A [0]=Y^B [0],
　　　　X [t]: Y^A [t]=YB [t] ==> Z^A [t]=Z^B [t],
　　　　X [t]: Y^A [t]=YB [t] ==> Y^A [t+1]=Y^B [t+1],
它将时序验证问题简化为用CA和CB实现的组合函数的比较。即如果从某一相同的初始状态出发，A和B等价所应满足的条件为其下一状态的等价及输出函数的等价：
　　 　　y'^A (y^A=y, x^A=x) = y'^B (y^B=y, x^B=x) ,
　　　　z^A (y^A=y, x^A=x) = z^B (y^B=y, x^B=x)
　　(3)用测试码自动生成的方法（ATPG）证明电路的等价性。利用ATPG的方法寻找图6.1电路的测试向量，如果能找到使异或输出为1的测试向量，则说明两个电路不等价。
　　对简单的电路，尤其是组合逻辑电路，证明其等价性以有比较有效的方法，如用BDD验证组合电路的等价性。而对于复杂的时序电路，还需要寻找更好的方法。对于不同级别的电路，要证明其等价性还是比较困难的事情,人们仍在研究。