控制数据流图结构变换的理论基础是算术操作与逻辑操作的结合律与分配律,其变换规则分别列于表5.8和5.9。
|
表5.8 结合律变换规则
|
| 类型 | Ⅰ | Ⅱ | Ⅲ |
| 1 | a + ( b + c ) | ( a + c ) + b | ( a + b ) + c |
| 2 | a * ( b * c ) |
( a * c ) * b | ( a * b ) * c |
| 3 | a + ( b - c ) | ( a - c ) + b | ( a + b ) - c |
| 4 | a * ( b / c ) | ( a / c ) * b | ( a * b ) / c |
| 5 | a - ( b - c ) | ( a + c ) - b | ( a - b ) + c |
| 6 | a / ( b / c ) |
( a * c ) / b | ( a / b ) * c |
| 7 | a - ( b + c ) | ( a - c ) - b | ( a - b ) - c |
| 8 | a / ( b * c ) | ( a / c ) / b | ( a / b ) / c |
|
表5.9 分配律变换规则
|
| 类型 | Ⅰ | Ⅱ |
| 1 | ( a + b ) * c | a * c + b * c |
| 2 | ( a - b ) * c |
a * c - b * c |
| 3 | ( a + b ) / c |
a / c + b / c |
| 4 | ( a - b ) / c | a / c - b / c |
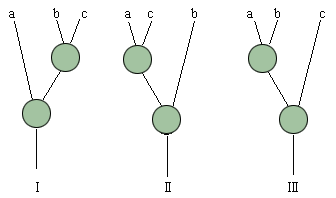
表5.8给出了算术操作结合律的3类、8种共24个变换规则。其中同一行的3个表达式恒等,同一列的8个表达式具有相同的数据相关性。这3类表达式对应的数据控制流图示于图5.36,这里给出的只是控制数据流图的局部结构,而结合律的变换也只影响控制数据流图相应的局部结构。
值得注意的是:部分结合律变换会引起相关操作类型的变化(例如表5.8中的变换5、变换6、变换7和变换8),从而导致控制数据流图中各操作类型数量的变化,适当利用这种变化可使硬件资源得到充分利用。图5.37是这种变换的实例。图(a)是变换前的控制数据流图,其中包含1个加法操作和3个减法操作,调度到2个控制步中。假设加法与减法分别用单个加法器和减法器实现,则需要1个加法器和2个减法器。对图(a)施加结合律变换5(I)→5(II),结果示于图 (b),其中含2个加法操作和2个减法操作,只需要1个加法器和1个减法器即可实现。对图(a)施加结合律变换5(III)→5(I),结果示于图 (c),其中含4个减法操作,可以用2个减法器实现。
|
图5.36 结合律变换3类表达式对应的控制数据流图结构
|