例1 请判断表5.1中操作12与操作13是否是互斥操作，其中 cv12 = {1, 0, X, X, 1 }
cv13 = { 1, 0, X, X, 0 }。
 |
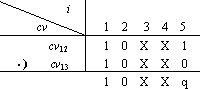cv=cv12·cv13 ＝{1, 0, X, X, X}
运算结果表明，操作13与操作14是互斥操作，其合并后的操作{12，13}的条件向量为{ 1, 0, X, X, X }。
例2 请判断表5.1中操作13与操作14是否是互斥操作，其中 cv13 = {1, 0, X, X, 0 } cv14= { 1, X, X, X, X } 。
 |
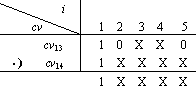cv=cv13·cv14 ＝φ
运算结果表明，操作13与操作14不是互斥操作，不能进行合并。
例3 请判断表5.1中操作5与操作12是否是互斥操作，其中 cv5 = {1, 1, X, 1, X } cv12 = { 1, 0, X, X, 1 } 。
 |
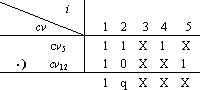结果中有q，满足条件（1），用X置换q，得：
cv=cv5·cv12 ＝{1, X, X, X, X}
运算结果表明，操作5与操作12是互斥操作，其合并后的操作{5，12}的条件向量为{ 1, X, X, X, X }。从合并后的条件向量看出，操作{5，12}只在条件a的分枝上，已从条件d及条件e的分枝上移出。
全局合并法建立在条件向量点积运算的基础上，通常用穷举或启发性策略进行。它可以全局地考虑互斥操作的合并，也可以考虑操作在条件分枝中的移动。
值得注意的是：对条件向量的点积运算稍加修改，全局合并法即可简化为局部合并法。点积运算经修改后成为叉积运算，记作cv1×cv2。
条件向量cv1与cv2的叉积运算记作cv1×cv2，其运算规则由叉积表（表5.3）和下列规则定义：
 |
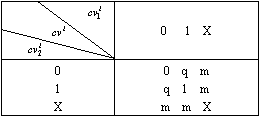(1) 如果
的结果中除{0,
1, X}外，有且仅有一个q时，则
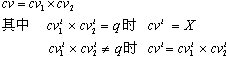
(2) 不满足条件(1)时：
cv=cv1×cv2=φ （条件向量叉积的结果为空）
两个条件向量的叉积运算中若出现m，表明相应的两个操作不在同一层次的条件分枝中。