图5.24中各操作的条件向量列于表5.1,其条件向量的维数为5。
| 操作 | 条件向量 {a,b,c,d,e} |
操作 | 条件向量 {a,b,c,d,e} |
| 1 | {0, X, X, X, X} | 8 | {1, X, X, X, X} |
| 2 | {1, 1, X, X, X} | 9 | {1, 0, X, X, X} |
| 3 | {1, 0, X, X, X} | 10 | {0, X, 0, X, X} |
| 4 | {0, X, 1, X, X} | 11 | {1, 1, X, 0, X} |
| 5 | {1, 1, X, 1, X} | 12 | {1, 0, X, X, 1} |
| 6 | {1, 0, X, X, 0} | 13 | {1, 0, X, X, 0} |
| 7 | {1, 0, X, X, X} | 14 | {1, X, X, X, X} |
全局合并法通过各操作的条件向量进行。设两个类型相同的操作为op1与op2(可以不是条件分枝中的操作),其条件向量分别是cv1与cv2,条件向量的维数为n。通过对条件向量的点积运算可以判断操作op1与op2是否互斥。
条件向量cv1与cv2的点积运算记作cv1·cv2,其运算规则由点积表(表5.2)和下列规则定义:
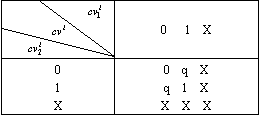 |
(1) 如果 ![]() 的结果中出现q时,则
的结果中出现q时,则
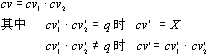
(2) 不满足条件(1)时:
![]() =φ (条件向量点积的结果为空)
=φ (条件向量点积的结果为空)
两个条件向量的点积运算结果若为空,表明这两个操作不是互斥操作;否则,他们是互斥操作,可以进行合并处理,点积运算结果就是合并所得操作的条件向量。