1.依据调度算法分类
在高层次综合中,最先提出的调度算法是Expl系统中的穷举法。此后又提出了许多算法,这些调度算法可以分为两类:
·变换法(transformation);
·构造法(constructive)。
变换法的基本思想是:首先找出一个初始调度方案,然后对该调度方案进行变换,以期得到最优调度。所谓变换就是将操作从一个控制步移到另一个控制步中。
图5.12给出了变换法的一个简单实例。图5.12(a)给出了初始调度方案,图5.12(b)是将操作5和操作6从cstep3移到cstep2后的结果,图5.12(c)是将操作3从cstep1移到cstep2后的结果。从图中看出,图5.12(a)所示初始调度方案需要3个加法器,在3个控制步内完成;图5.12(b)所示调度方案需要3个加法器,在2个控制步内完成;图5.12(c)所示调度方案需要2个加法器,在3个控制步内完成。
这个例子表明,对初始调度方案加以适当变换,可以得到更理想的调度结果:或者减少所需控制步数;或者减少对硬件资源的需求。
图5.12 调度中的变换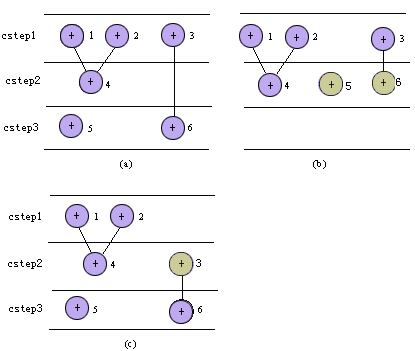 |
变换的方法通常有穷举法和启发式方法两类。穷举法可以找到调度的最优解,但计算量庞大。穷举法可以通过分枝定界法(branch
and bound)加以改进,但计算量仍较大,只适合于规模较小的设计。 穷举法的另一种的改进方法是,只有数据相关性和约束条件允许时,才进行操作的移动。
常用的启发式变换方法是模拟退火法(simulated annealing)。启发式变换方法的目的是以较小的计算量来寻求近似最优解或满意解。
构造型调度算法的基本思想是:每次选择一个操作进行调度,直至所有操作均被调度为止 。构造型调度算法的关键在于:如何选择下一个被调度的操作,以及把所选定的操作赋给哪一个控制步。构造型调度算法的实质是利用启发式策略寻求近似最优解或满意解。构造型调度算法也可以转化为组合最优化问题(如整数线性规划问题)去求解。