3. 划分等价类的逐次分割法
　　此方法又称K等价划分法。因为用K来标志当前是第几次分割。它是实现最小化输出一致的置换性划分的一个有效算法，缺点是效率不太高。
　　Step1 　令K = 1;
　　按照输出一致的要求对S进行划分，即把每一输入组合Ip作用下输出相同的状态归入同一类，形成 π1 。
　　Step2 　令K = K + 1; 作πk =πk-1；
　　按照置换性划分的要求对πk继续进行划分：对于πk中每一个类Si（Si∈πk）, 在每一输入组合Ip作用下，凡siq∈Si的后继状态能落入πk-1 的同一类中者，构成一个新类。然后用这若干个新类代替Si 。
　　Step3　若πk =πk-1 , 算法结束，πk即为所求结果。 否则，转Step2。
　　举例：表4.15描述的时序机的状态集为：
　　　　　　　　　　　　S = { a , b , c , d , e }
　　求其输出一致的置换性最小划分。
　　Step1 　K = 1;
　　　　　　　　π1 = {(a , b , c),(d , e)};
　　Step2 　K = K + 1 = 2;
　　　　　　　　π2 = π1 = {(a , b , c),(d , e)};
　　对π2中每一个类继续进行划分：
　　（1）检查(a , b , c)：在输入信号In = 1 时，
　　因此，用 {( a ,b) ,(c)} 代替{(a ,b ,c )}
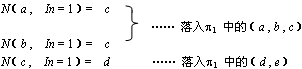
　　（2）检查 ( d ,e )
　 因此，(d，e)保持不变。
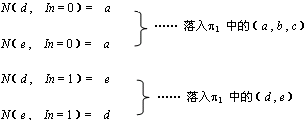
　　于是， π2 = {(a ,b),(c),(d,e)}
　　Step3 　π2≠π1 　转Step2
　　Step2'　K = K + 1 = 3;
　　　　　　 π3 = π2 = {(a ,b) ,(c),(d ,e)}
　　对 π3 中每一个类进行检查，均符合置换性划分的要求，故不再继续划分。
　　Step3'　因 π3 = π2 , 算法结束， π3 就是最终结果。