通常采用状态表或状态图来描述有限状态机的输出和状态迁移的情况。举例说明如下：设某个有限状态机的所有可能的状态集合为：
　　　　　S = { a，b，d，e }
　　其输入信号In的所有可能输入组合为：
　　　　　I = { 0, 1 }
　　其输出信号Out的所有可能输出组合为：
　　　　　Z = { 0, 1 } 　　
　　
表4.15 时序机（Mealy模型）状态表举例

当前状态
State
输入信号
In
后继状态
Next
输出信号
Out
a
0
b
0
a
1
c
0
b
0
a
0
b
1
c
0
c
0
a
0
c
1
d
0
d
0
a
1
d
1
c
1
e
0
a
1
e
1
d
1

图4.16 时序机状态图举例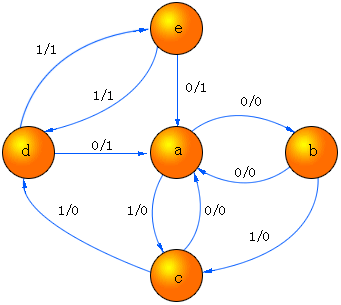
　　
　　表4.15 表示该有限状态机（Mealy模型）输出和状态的迁移情况。与状态表相对应的另一表示法是时序机的状态图，示于图4.16。图中的结点（圆圈）代表一个特定的状态，有向弧表示在某种输入下输出和状态的迁移情况，并以 Ip / Zk 的方式在有向弧的旁边注明相应的输入和输出。经过对照后。读者会发现表4.15和图4.16是同一时序机。
　　时序机模型除了Mealy 模型外，还有一种Moore模型；两种模型可以互相转化，限于篇幅，对于Moore模型，此处不作介绍。
　　状态表（参见表4.15）中若在每一输入组合情况下，其次态Next和输出Out都是唯一确定的，则称该时序机为完全规定的有限状态机（或完全规定的时序机）；否则是不完全规定的有限状态机（或不完全规定的时序机）。所谓不确定是指次态Next一栏出现了未明确指定的状态（用 表示）；或输出Out一栏出现了未明确指定的值（用u表示）。
　　时序机综合的步骤如下：
　　（1）建立原始状态图（或状态表），描述时序机的输出和状态的迁移情况。
　　（2）状态化简：把原始状态图（或状态表）中的冗余状态删除；把可以合并的状态加以合并。寻求一个功能（状态表）等价的、状态数目最小或接近最小的时序机。
　　（3）状态分配：将最小状态表中每个状态分配一个状态变量的编码，目标是造价最低。
　　（4）用组合逻辑电路综合的方法，实现次态函数N和输出函数Z。