·G算法 　　
　　 G算法以M(γ)最大为目标。在覆盖C中立方体之间求一公因子γ。
　　　(1) 覆盖C中每一立方体的初始高度h都为1，标明其高度h和优值M。
　　　(2) 令 　γ= XX…X…X
　　　　　　　　M(γ) = O
　　　(3) 从覆盖C中选一优值M最大的元素c。
　　　(4) c和覆盖C中其它任一元素作m积，并标明其高度h和优值M。
　　　(5) 从诸m积中选出一优值最大者 。
　　　(6) 用β代替覆盖C中由m积形成 的两个元素。
　　　(7) 若 M(γ) < M (β)
　　则令 　　M(γ) = M (β)
　　　　　　　γ= β
　　　(8)若覆盖C被简化到只有一个立方体时则停止，否则转入(3)。
　　由以上步骤求出的公因子 其优值最大或接近最大。下一步应当把C分解为两个子集S和N，并进一步提取公因子。这一过程在H算法中已有说明，不再赘述。
　　本节介绍了几种提取公因子的算法，可以解决扇入约束问题，并且把二级逻辑转化为多级逻辑，但它还不能说是一个优秀的算法。
　　把布尔函数转化为多级逻辑电路的方法还有其他方法，比较有代表性的有：
　　·先农展开定理（Shannon's Expansion Theorem）：
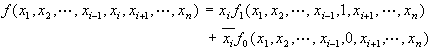
　　 这种方法适合于手工作业。
　　·二叉判决图（Binary Decision Diagram, BDD）：
　　BDD是基于先农展开的图形表示，当把输入变量的顺序排定之后。BDD就变成有序的BDD（Orded BDD, OBDD）。OBDD适合于计算机作业。OBDD已经应用于多级逻辑综合和形式验证。
　　限于篇幅，本书对这些方法只能简单地提及。