·H算法
H算法以h(
也就是说 是S中每一元素的因子。
S=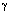 ∩D
∩D
D是对S提取公因子 后的剩余部分
把二级电路转化为多级电路是一个反复提取公因子的过程.下一步则应当对D和N分别提取公因子…….直到提不出新的公因子时为止。
以下叙述对覆盖C提取一个公因子的详细步骤:
(1) 形成覆盖c的列高度函数:
h(0) = a1a2 ...ai... an
h(1) = b1b2 ...bi... bn
式中ai是一整数,代表覆盖C中变量xi取值为0的个数;bi代表C中变量xi取值为1的个数。
(2) 求出最大列高度:
ak = MAX(a1a2... ai... an ) k∈(1, 2,... n )
bj = MAX(b1b2 ...bi... bn ) j∈(1, 2,... n )
(3) 若ak < 2且bj < 2则停止。
(4) 若ak > bj则 k = 0且 i = X ( i≠k ) ;
否则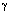 j
=1且
j
=1且 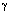 j
=X (i≠j )。
j
=X (i≠j )。
实例:设覆盖C为:
S=
D是对S提取公因子 后的剩余部分
把二级电路转化为多级电路是一个反复提取公因子的过程.下一步则应当对D和N分别提取公因子…….直到提不出新的公因子时为止。
以下叙述对覆盖C提取一个公因子的详细步骤:
(1) 形成覆盖c的列高度函数:
h(0) = a1a2 ...ai... an
h(1) = b1b2 ...bi... bn
式中ai是一整数,代表覆盖C中变量xi取值为0的个数;bi代表C中变量xi取值为1的个数。
(2) 求出最大列高度:
ak = MAX(a1a2... ai... an ) k∈(1, 2,... n )
bj = MAX(b1b2 ...bi... bn ) j∈(1, 2,... n )
(3) 若ak < 2且bj < 2则停止。
(4) 若ak > bj则 k = 0且 i = X ( i≠k ) ;
否则
实例:设覆盖C为:
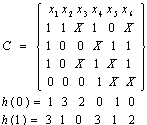
最大列高度
a2 = 3
b1 = 3
提取公因子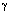 =
1 X X X X X
=
1 X X X X X
把C分解为:
a2 = 3
b1 = 3
提取公因子
把C分解为:
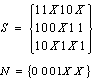
对S提出公因子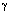 后,剩余部分为D:
后,剩余部分为D:
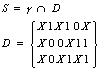
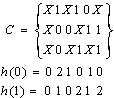
a2 = 2
b4 = 2
提取公因子
把C分解为:
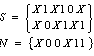
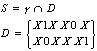
![]()