·优值M(γ)
表示在成本方面因提取公因子 而得到的收益。
·m积(mask product)
设 a = c1c2 cicn
| d1d2djdm
b = e1e2eien| f1f2fjfm
m积的定义如下:
(1)若ci= ei 则 (ci) m (ei) = ci
否则 (ci) m (ei) = X
(2)若dj= fj 则 (dj) m (fj) = 1
否则 (dj) m (fj) = u
例1
10X11 | 1u1u ...a
m) 101X0 | 111u ...b
----------------------------------------------------
10XXX | 1u1u ...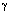
b = e1e2eien| f1f2fjfm
m积的定义如下:
(1)若ci= ei 则 (ci) m (ei) = ci
否则 (ci) m (ei) = X
(2)若dj= fj 则 (dj) m (fj) = 1
否则 (dj) m (fj) = u
例1
10X11 | 1u1u ...a
m) 101X0 | 111u ...b
----------------------------------------------------
10XXX | 1u1u ...
例2
11011XX | 1 ...a
m) 1111000 | 1 ...b
----------------------------------------------------
11X1XXX |1 ...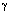
m积的结果 是立方体a, b的公因子。因为立方体和因子都是以立方体形式表示的,所以因子和立方体或因子和因子之间进一步求公因子时也可用m积。并且
h(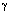 )
= h(a) + h(b)
)
= h(a) + h(b)
11011XX | 1 ...a
m) 1111000 | 1 ...b
----------------------------------------------------
11X1XXX |1 ...
m积的结果 是立方体a, b的公因子。因为立方体和因子都是以立方体形式表示的,所以因子和立方体或因子和因子之间进一步求公因子时也可用m积。并且
h(
W算法是以宽度最大为目标在两个立方体(因子)之间求公因子。然后在因子之间进一步求公因子.直到提不出公因子时为止.为了简明起见,以下步骤是以单输出函数的形式叙述的。
(1) 从覆盖C中选一宽度最大的元素c。
(2) c和C中其它任一元素作m积,从诸m积中选一宽度最大者作为本次提出的公因子 。
(3) 记下公因于 和形成 的两个元素。
(4) 从覆盖C中删去形成 的两个元素,以 代替它们。
(5) 若覆盖C被简化到只有一个元素时停止,否则转入(1)。
实例:
|
|