一个立方体的成本(造价)可表示为：
　　　　　　cs（c）= n - r
　　其中n代表该立方体c的输入变量个数，r代表c的维数。若用一个与门和-个立方体相对应，则cs(c)代表该与门的输入端数，若
　　　　　　cs(c) > FI
　　就是超出了扇入限制条件。　　
　　实例：设函数f的最小化覆盖C为：　　　　
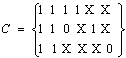
　　　写成布尔表达式
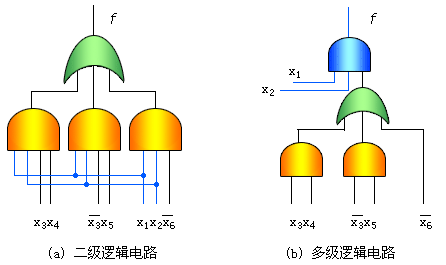
　　　对应的电路图示于图4.14(a)，共需4个门，14个输入端。提取公因子后：
　　　对应的电路示于图4.14(b)，共需4个门，10个输入端。由此可见，提取公因子后可导致：
　　　(1)元件的输入端减少，可解决扇入FI所带来的限制。同时也缓解了扇出FO所带来的限制。
　　　(2)成本有可能降低。
　　　(3) 逻辑级数有可能增加，即电路的总延迟时间可能增加。
　　　本节重点讨论如何用立方体运算提取公因子。
图4.14 二级电路转化为多级电路的实例


　　
　　　前面的例子是用手工方法提取公因子，其对应的立方体表示形式为：
　　　　　　　　C＝∩D
　　　其中是公因子，即：
　　　　　　　　 = 11XXXX （公因子为x1x2）
　　　D是从C中提取公因子 后的剩余部分。
　　形成D的方法是：对c中每一元素e作如下改变：若某个变量在 中取值不为X(1或0)，则把它在e中的取值改为X。
　 设立方体表示为：
　　　　　　　　　　　　　　　　
　 　

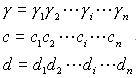
　　 若 c
　　 则称是c的因子。
　　 若 c 　且　d
　　 则称是c和d的公因子。
　 　设覆盖C中元素的个数为m， 是其中h个元素的公因子，则称h()是公因子的高度。并称
　　　　　　w() = cs()
　 　为的宽度。