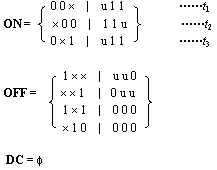
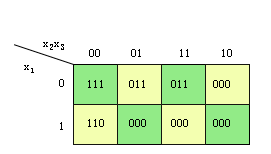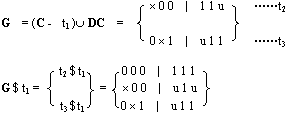
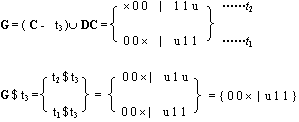
· E算法 　　设 C是布尔函数F的覆盖表示形式，p是F的质蕴涵项，令 　　　　G = ( C - {p} ) ∪ DC （4-16） 　　则 p 是F的必要质蕴涵项的充要条件为： 　　　　（p ∩ ON í G $ p） = false （ 4-17） 　　实例: 图4.12是多输出布尔函数的卡诺图，其覆盖形式为： 　　　　 图4.12 3输入3输出布尔函数卡诺图 　　 　　准备工作，令 C = ON 　　已知： t1= 0 0 ×| u 1 1 　　是质立方体，欲知t1是否是必要质立方体，其判别条件为式（4-17）。 　　　　 　　　　t1∩ON = 0 0 ×| u 1 1 　　因为： t1∩ONG $ t1 　　所以t1不是必要质蕴涵项。 　　此外，已知t3是质立方体，欲判别t3是否是必要质立方体，作： 　　　　 　　　　t3∩ON = 0×1| u 1 1 　　因为： t3∩ONG $ t1 不成立， 　　所以t3是必要质蕴涵项。