删除多余连线 j从1到m重复以下步骤m次：
　　(1) 从C中分离出y^j取值为1的立方体(仅输入部分)集合CON^j，从N中分离出y^j取值为1的立方体(输入部分)集合NON^j。
　　(2) 对NON^j中每一元素e进行检查，若：
　　　　　　{e#(NON^j-e)}∩CON^j=φ
则将N中对应元素(其输入部分等于e)的输出变量y^j的取值由1改为u。且：
　　　　　　NON^j = { NON^j - e }

　　实例：设多输出函数f的初始覆盖C为：
　　　　　　
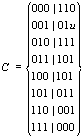
　　首先从初始覆盖C中分离出CON：
　　　　　　
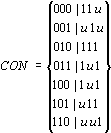
　　第一步 N = S{CON} = CON
　　第二步
　　　　　　
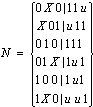
　　第三步 010 | 111是冗余立方体，把它从N中删除。
　　　　　　
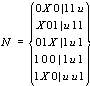
　　第四步 删除多余连线：
　　　　　　
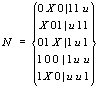
　　为了说明删除多余连线的物理意义，画出对应的电路图示于图4.11(a)．图中的红色虚线起作用时对应于第三步的结果，虚线被删除时对应于第四步的结果．由此可知，经过删除多余连线这一步骤进一步降低了成本。但是，未经这一步化简时立方体100 | 1u1是质立方体，经过这一步之后，100 | 1uu却反而不是质立方体了。由此可知，还存在着进一步降低成本的可能性。

图 4.11 多输出函数化简中的删除多余连线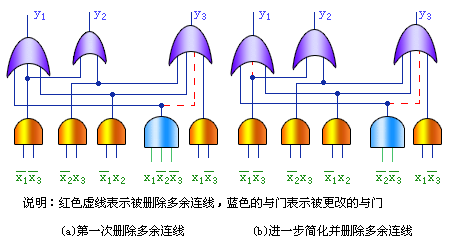

　　第五步 把第四步修改过的立方体
　　　　　　e′= 100 | 1uu
　　转化为质立方体：
　　　　　　z ＝ X00|1uu
　　用 z 代替e′：
　　　　　　
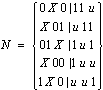
　　返回第三步，N没发生变化。
　　第四步又可删除多余连线，其结果为：
　　　　　　
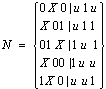
　　第五步 N没发生变化，这个解就是最终解。它所对应的逻辑图见图4.11(b)。
　　图中虚线表示多余连线，是经过删除多余连线这一步骤之后才发现它是多余连线。由此可见删除多余连线这一步骤的必要性。