Untitled Document

　　
　　· 极值(extremal)
　　设SZ是Z的一个子集，e是SZ的一个元素，若e包含了某个不被SZ中其它元素所包含的真值顶点，则称e为极值。
　　若： {e#(SZ-e)}∩CC≠φ　(e∈SZ)　　(4-13)
　　则e是一个极值。式中CC是立方体的集合，它包含且仅包含全部待包含的真值顶点，用选拔法实现最小化覆盖时，极值应当被选为M的元素。理由是每个真值顶点都应当被M包含，而包含该真值顶点的诸立方体中，e的成本最低，因为质立方体和它的面相比成本较低。
　　· 小于 运算(1ess than)
　　小于运算是对立方体集合A中的元素逐对进行比较，设被比较的两个元素是aⁱ和a^j，若：
　　　　(1) aⁱ的成本 ≥ a^j的成本
　　　　(2) ( aⁱ#a^j )∩CC=φ
　　则说aⁱ小于(劣于) a^j，并从A中把aⁱ删除。由此可知，小于运算实际上是删劣运算。对A作小于运算记作：lt(A)
　　选拔法实现最小化覆盖的步骤如下：
　　第一步令 CC = CON
　　　　　　　SZ = Z
　　　　　　　M =

　　第二步反复执行以下步骤：
　　(1) 令SZ = lt(SZ)
　　(2) 令E =

　　(3) 对SZ中每一元素e作极值判断。若：
　　　　　{e#(SZ-e)}∩CC≠φ　(e∈SZ)
　　则e是极值项。作：
　　　　　E=E∪e，SZ=SZ-e，CC=CC#e
　　(4) 令M＝M ∪ E ，
　　(5) 若CC =

则M就是最小化覆盖，结束。
　　(6) 若E ≠

转去执行(1)，进入下一轮选优。否则，执行下一步。
　　第三步分枝处理(branch)，进入这一步的前提是CC≠

，即M还未能包含全部真值顶点；此外，E =

，即选不出极值。这种情况称为循环状态。需要采用启发式的方法，从SZ中选一个质立方体p:
　　(1) 路径1：从SZ中任选一立方体p，把它当作极值。于是：
　　　　　　E= { p }
　　　　　　SZ= SZ - p
　　　　　　CC= CC # p
转去执行第二步(4)，得到一个包含p的解，记作M( p )。当然，在此过程中还可能遇到新的分枝，可按同样方法处理。
　　(2) 路径2：与路径1的假定相反，认为p劣于SZ中另一个质立方体，从而把p从SZ中删除，于是：
　　　　　　SZ= {SZ - p}
转去执行第二步(2)，得到一个不包含p的解，记作 M(p)。
　　显然，最小化解必是M(p)或 M(p)中的一个。从中选成本较低者作为最终解。

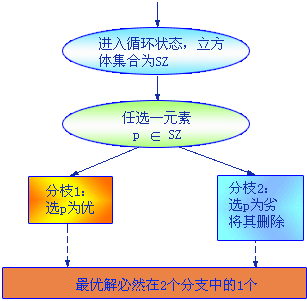
　　上述分枝法处理循环状态可用示意图表示如下：