Untitled Document

　　
　　表4.11 星积运算表

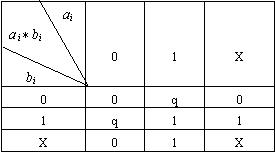　　例1 a = 1XX b = 0X1 求a * b。

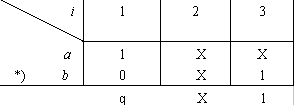　　注意到上述运算结果中只有一个q，满足条件（1），用X去置换q，得:
　　　　c = a * b = XX1
此运算结果见图4.7。

　　例2 a=01X b=11X求a * b

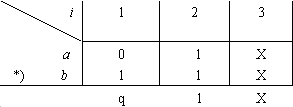　　注意到上述运算结果中只有一个q，满足条件（1），用X去置换q，得：
　　　c = a * b = X1X
此运算结果见图4.8。

　　例3 a=XX1 b=0X1求a * b

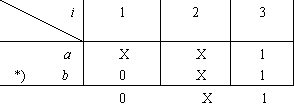　　注意到上述运算结果中q的个数为0，不满足条件（1），故:
　　　　c = a * b =

　　· 星积运算的目的是求质立方体，见4.4.2和4.4.3节，星积运算求质立方体实际上是对表格法（Quine-McCliskey方法）的改进，有关表格法的介绍见《数字逻辑及数字集成电路》一书。
　　· 星积运算的特点是根据两个已知的立方体求一个新立方体，新立方体一定和原来的立方体不同。新立方体的维数可能增大也可能不增大，但是通过反复作星积运算就有可能求出维数更大的立方体。

　　当我们用两个二进制数代表一个立方体，并采用表4.3中方案二的表示法时，星积运算的实现方案如下(采用符号同4.2.2节)；
　　(1) 作: w = ( a_i XOR b_i ) AND ( a_j XOR b_j )
　　(2) 若: w = 0 则 c = , 算法结束。（解释：w = 0 意味着 q 的个数为 0）
　　(3) 若： (w ) AND (w - 1 ) = 0 则：（解释：此条件意味着 q 的个数为 1 ）
　　　　　c_i = (a_i AND b_i ) OR ( w )
　　　　　cj = (a_j AND b_j ) OR ( w )
　　　　否则： c =