实例：　a = X0XX b = 1X01 求a # b和a b
　　　　　　X0XX ……a　　　　　　X0XX ……a
　　　　#)　1X01 ……b 　　　)　1X01 ……b
　　-------------------------------------------------
　　　　　　00XX　　　　　　　　　00XX
　　　　　　X01X　　　　　　　　　101X
　　　　　　X0X0　　　　　　　　　1000
　　对应的卡诺图见图4.6。

图 4.6 锐积和不相交锐积的比较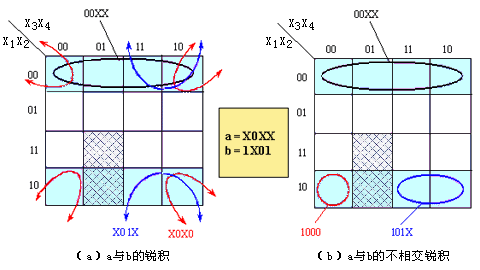

　　积的用处是：
　　(1) 用来计算顶点数。因为积结果中的各立方体互不相交，所以包含顶点之总数等于各立方体包含的顶点数之和。而每个立方体包含的顶点数为2^r，其中r是该立方体的维数。
　　(2) 在覆盖与覆盖、覆盖与立方体作积运算时，运算速度较#积快。
　　#积较积的优点是：在求质立方体时可以用# 积而不能用积。
　　当我们作多输出函数不相交锐积的时候，可以这样设想；
　　　　(1) 首先把多输出函数转化为单输出函数。
　　　　(2) 对每个单输出函数作不相交锐积运算。
　　　　(3) 把第（2）步的结果合并成多输出函数的表示形式。
假如第(3)步的结果和下述多输出函数锐积运算规则的结果等价，那么这个规则就是正确的。
　　规则1 若(a | b)和(c | d)是分离的，则 (a | b)(c | d) ＝ (a | b)
　　规则2 若ac 则(a | b)(c | d)=(a | e)。
　　　　　若：b^j = β∈{0, 1} 且d^j = u ( j从1到m )
　　　　　则: e^j = b^j
　　　　　否则: e^j = u
　　规则3 若上述规则都不满足，则(a | b)(c | d)的结果由下列立方体组成：
　　(1) a | g
　　　　　若： d^j = u (j从1到m)
　　　　　则： g^j = b^j
　　　　　否则：g^j = u
　　(2) （i从1到n）
　　　　　若：a_i c_i= α_i∈{ 0, 1 } 则对应于一个立方体fⁱ：
　　　　　　　fⁱ=(a₁∩c₁)(a₂∩c₂) …(a_i-1∩c_i-1)α_ia_i+1…a_n
　　　　　而