例1 a | b = 1011 | u10
c | d = 0X11 | 10u
因a | b与c | d是分离的,满足规则1
∴(a | b) # (c | d) = (a | b) =1011 | u10
例2 a | b = 1011 | 1u0
c | d = 1X1X | 10u
不满足规则1,但满足规则2,( 因a
∴(a | b) # (c | d) = (a | e) =1011 | uu0
例3 a | b = X0X1 | 1u1
c | d = 1X01 | 11u
既不满足规则1,也不满足规则2。
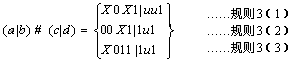
对多输出函数的锐积运算,只要求理解不要求证明。
· 书中给出的算法描述比较精练,适合于编程(算法指导编程,因而算法必须精练)不适合于理解。怎样理解其正确性呢?
可以设想:把多输出函数拆成多个单输出函数,对每一个单输出函数作锐积运算,最后再把他们合并起来成为多输出函数。
· 更好的方法是编写一段程序,按书中描述的算法实现多输出 / 单输出函数的锐积,输入数据,观察输出结果是否符合锐积的定义。