锐积运算的结果是一个立方体的集合C。由a包含的顶点减去a∩b包含的顶点所形成的维数最大的立方体都是C的元素。
　　　　　　K0(C)=K0(a)-k0(a)∩K0(b)　　(4-9)
　　由此可知，当a和b不相交时：
　　　　　　k0(a)∩K0(b)＝（空集）
　　　　　　K0(C)=K0(a)
　　所以　　a # b = a
　　当b包含a时：
　　　　　　k0(a)∩K0(b)＝k0(a)
　　　　　　K0(C)=（空集）
　　所以　　a # b =
　　锐积运算可由表4.10和下述规则来定义。 　　
表4.10 锐积运算表


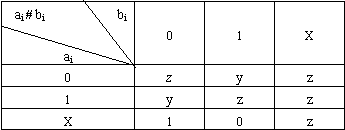　　(1) 若存在一个i (i从1到n)能使ai # bi= y成立，则
　　　　　　a # b = a
　　这条规则是说当a和b不相交时，a # b = a。
　　(2) 若对所有的i (i从1到n)都使ai # bi = z成立，则
　　　　　　a # b =
　　这条规则是说当ab 时，a # b =φ。
　　(3) 不满足以上条件时，若有:
　　　　　　ai # bi= αi∈{ 0,1 }
　　则对应于一个立方体fi：
　　　　　　fi＝a1a2…ai-1αiai+1…an
　　于是：
　　　　　　a # b ={fi}
　　　　　　a # b ={a1a2…ai-1αiai+1…an}