Untitled Document

　　
　　我们已经介绍过用二进制数表示立方体的方法，也介绍过立方体相交和包含判断的规则。所以，实现立方体运算的问题已经解决。但是，如果用字符表示立方体的每一位，按位用字符作运算，速度很慢。所以，立方体运算还是要用二进制数作运算，而不是用字符作运算。限于篇幅，只以表4.3中的立方体表示法为例，而不再介绍其它的表示方法和比较它们的优缺点。同样的理由，我们只以输入部分为例来介绍这些运算的实现方法。虽然输出部分包含的判断规则与输入部分包含的判断规则不同，相信读者在读完本节之后有能力解决这个问题。
　　设有两个立方体:
　　　　　a = a₁a₂...a_k...a_n
　　　　　b = b₁b₂...b_k...b_n
　　其相交的结果为立方体c:
　　　　　c = c₁c₂...c_k...c_n
　　我们用两个二进制数合起来代表一个立方体。(ai，aj)代表立方体a，(bi，bj)代表立方体b，(ci，cj)代表立方体c：
　　　　　ai = ai₁ai₂...ai_k...ai_n
　　　　　aj = aj₁aj_2...aj_k...aj_n
　　　　　bi = bi₁bi₂...bi_k...bi_n
　　　　　bj = bj₁bj₂...bj_k...bj_n
　　　　　ci = ci₁ci₂...ci_k...ci_n
　　　　　cj = cj1cj2...cjk...cjn
　　现在把立方体表示法中第k位的各种取值及其特征列于表4.8(方案一)和表4.9(方案二)。仔细分析该表可得出对应的运算规则。
　　　　　　　　　　　　　表4.8　　相交运算和饱含判断（方案一）
　　　　　　　

　　　　　　　　　　　　　　表4.9　　相交运算和饱含判断（方案二）　　　　　　　　　
　　　　　　　　

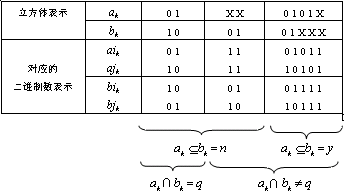
　　　表4.8和表4.3中的方案一相对应，这种情况下的相交运算规则是：
　　　　(1)若：(ai XOR bi) AND (aj XOR bj) = 0
　　　则立方体a和b相交。　　　c=a∩b
　　　　　　　　　　

　　　　上面所用符号：
　　　　　　　　　　　XOR表示按位作异或运算
　　　　　　　　　　　AND表示按位作逻辑与运算
　　　　　　　　　　　OR表示按位作逻辑或运算
　　　　(2)若条件(1)不满足，则立方体a和b不相交；
　　　　　包含的判断规则是：若下述两个条件
　　　　　　　　　　　

　　　　　成立，则：
　　　　　　　　　　a

b
　　　　　表4.9和表4.3中的方案二相对应，这种情况下的相交运算规则是：
　　　　　(1) 若：(ai XOR bi) AND (aj XOR bj) = 0
　　　　则立方体a和b相交。　　　c=a∩b
　　　　　　　　　　　　

　　　　　(2) 若条件(1)不满足，则立方体a和b不相交。
　　　　　　包含的判断规则是：若下述两个条件
　　　　　　　　　　　　

　　　　　　成立，则：
　　　　　　　　　　　a