例:图4.3所表示的布尔函数f的覆盖C可表示为:
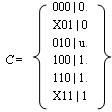
求C的立方复合体K的步骤如下:
(1) C中的每一个立方体都属于K:
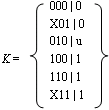
(2)求出K中每一个立方体的面;
X01| 0的面是: ![]()
11X | 1的面是: ![]()
X11 | 1的面是: ![]()
(3) 求出K中每一个立方体相对于覆盖C的余面;
000 | 0的余面是: ![]()
X01| 0无余面
010 | u的余面是: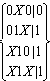
100 | 1的余面是: {1 X 0|1}
110 | 1的余面是: {X 1X | 1}
X11 | 1的余面是: {X1X | 1}
(4)将K中每一个立方体的余面加入K:
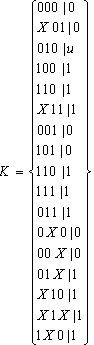
请注意,余面0X0|0和余面01X|1,X10|1以及X1X|1相互矛盾,不具备一致性。但是它们中的每一个和覆盖C一致,并不矛盾。
本例中的质立方体是:X01|0,0X0|0,00X|0,1X0|1和X1X|1。