·立方体的相交运算(intersection)
单输出函数的立方体a和立方体c的"交"是它们的公共顶点所组成的立方体。多输出函数的立方体a|b 和立方体c| d的"交"是单输出函数"交"运算的扩展。若两立方体之间无公共顶点,则说它们是分离的。相交运算符用"∩"表示。两个立方体的相交运算可由表4.6和表4.7和下述规则来定义:
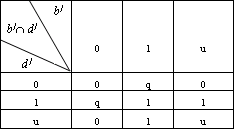
(1) 输入变量的对应元素按表4.6作相交运算;输出变量的对应元素按表4.7作相交运算。
(2) 若所得结果中有任一元素为q,则称此相交运算的结果为退化立方体。
(3) 若相交运算的结果为退化立方体,且结果中输入部分有任一元素为q,则称此结果为空立方体,记作
表4.6 相交运算表A
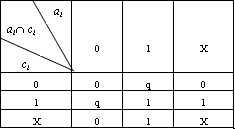
表4.7 相交运算表B
单输出函数的立方体a和立方体c的"交"是它们的公共顶点所组成的立方体。
多输出函数的立方体a| b 和立方体c| d的"交"是单输出函数"交"运算的扩展,但多输出函数的"交"运算不再具有"公共顶点"的含义。我们只把它看作一种有用的运算,可用于"一致性"判断。
·一致性(consistence)
两个立方体作相交运算时,若其输出部分出现q而其输入部分不出现q的话,则称此二立方体是不一致的,反之,它们是一致的。
用立方体定义函数时,立方体之间必须具备一致性。只有这样,才能确保不同立方体的输入部分的共同部分不会有矛盾的输出值。因此在作逻辑综合之前,首先应对原始数据作一致性检查。若发现不一致性,则应纠正原始数据中的错误。
一致性就是不矛盾性。用真值表描述布尔函数时不会出现不一致性,因为真值表中是对每一个最小项分别进行描述。用覆盖表描述布尔函数时就比较容易出现不一致性,因为覆盖表中是对每一个立方体分别进行描述。一个立方体可能包含多个最小项,一个最小项可能被多个立方体包含。如果不小心,某个最小项的取值可能在这里被隐式定义为1,而在另外一个地方被隐式定义为0。如果出现这种前后矛盾的原始描述,后续工作就无法进行。这就是逻辑综合之前必须对原始数据作一致性检查的原因。
例1
1 X 1 1 | 1 u 1
∩) 0 1 X 1 | u 1 u
--------------------------------------------------
q 1 1 1 | 1 1 1
相交结果为空立方体,具备一致性。
例2
0 X 0 X | 1 u 1
∩) X X 0 1 | 0 1 u
--------------------------------------------------
0 X 0 1 | q 1 1
相交结果为退化立方体,不具备一致性。
这是一个不满足一致性要求的具体例子,对于函数f1而言,顶点(最小项)0001的取值到底是0还是1 ?
第一个立方体规定它是1。
第二个立方体规定它是0。
同理,两个立方体对顶点0101取值的规定也是矛盾的。
例3
1 1 X 1 | 0 u 1
∩) 1 X 1 0 | 1 0 u
--------------------------------------------------
1 1 1 q | q 0 1
相交结果是退化立方体,也是空立方体,具备一致性。