设布尔函数的一般表示形式为：
y = f(x1,x2,...xi,...xn)
其中y为输出变量，xi为输入变量。令每一输入变量和一个坐标轴相对应，则可得到函数y的空间图形。今以n = 3为例，建立起卡诺图和立方体符号之间的对应关系，如图4.3所示。每一最小项对应于卡诺图中的一个最小方格，对应于立方体中的一个顶点。取值为0的最小项在图4.3(a)中对应的小方格中填0，在图4.3(b)中对应的顶点画上蓝色圆圈。取值为1的最小项在图4.3(a)中对应的小方格中填1，在图4.3(b)中对应的顶点画上红色圆圈。取值为d的最小项在图4.3(a)中对应的小方格中填d，在图4.3(b)中对应的顶点画上星号。
当变量个数大于3时，立方体图形很难表示。有人把变量个数大于3的立方体称为超立方体，本书则一律称立方体。
图4.3 卡诺图与立方体的对应关系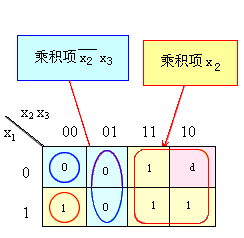 图（a） |
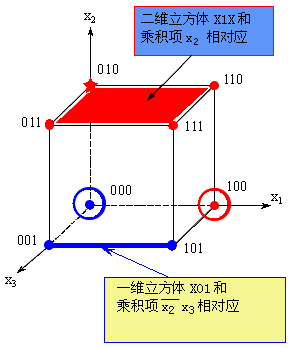 图（b） |
卡诺图中相邻的两个小方格可以合并，例如图4.3(a)中的乘积项
在图4.3(b)中对应于连接这两个顶点的一条棱，记作(X01)。这里用1代表原变量，0代表反变量，X代表因合并而消去的变量。同理，卡诺图中乘积项x2(由四个最小方格合并而成)对应于立方体图形中由此四个顶点组成的一个面(X1X)。我们用被消去的变量个数来代表立方体的等级，于是：(X1X)是2维立方体，对应于立方体图形中的一个面；(X01)是一维立方体，对应于一条棱；(100)是0维立方体，对应于一个顶点。一个布尔函数的全部0维立方体的集合用K0表示，全部一维立方体的集合用K1表示……，全部r维立方体的集合用Kr表示，Kr的元素是立方体x，x的一般形式为：
x = x1, x2, xi, xn xi∈{ 0, 1, X }
其中取值为X的因子有r个。由于每个输入变量的取值有三种可能，故不能简单地用二进制数表示。
办法之一是让二进制数中相邻的两位合起来共同代表立方体表示法中一个变量的取值，例如：
二进制数a:
立方体x: x1 x2 xk xm
办法之二是用两个二进制数合起来共同代表一个立方体，例如：
二进制数i: i1, i2, ...ik,... in
二进制数j: j1, j2, ...jk, ...jn
立方体x: x1, x2, ...xk, ...xn
本文以后的例子均采用后一种办法。ik，jk和xk的对应关系可有多种，表4.3表示了其中的两种。
|
二进制数第k位的取值
|
ik
|
0
|
0
|
1
|
1
|
|
jk
|
0
|
1
|
0
|
1
|
|
|
立方体表示法中对应的变量ci的取值
|
方案之一
|
0
|
x
|
/
|
1
|
|
方案之二
|
/
|
0
|
1
|
x
|
怎样在计算机内部表示立方体呢？可以用字符，也可以用二进制数。相比之下，用二进制数更节省存储空间，运算速度也更快。
表4.3列举了两种表示法，目的是为了具体。读者也可以试用其他表示法。