|
表4.2 覆盖表之一例
|
 |
组合逻辑电路综合的基本方法是：把设计者的原始描述转化为覆盖表，然后将覆盖表化简，最后找寻一个与化简了的覆盖表相对应的组合逻辑电路。
覆盖表的化简基于布尔函数的化简，为此我们要复习一下布尔代数中的一些基本概念和重要术语，并对之作出严格的定义。
最小项(minterm)
设
是n个布尔变量，p为n个因子的乘积。如果在p中每一变量都以原变量
或反变量
的形式作为因子出现一次且仅出现一次，则称p为n个变量的一个最小项。例如，有三个布尔变量
和
，则
是最小项；而
不是最小项，因为
或
都没有作为因子出现于p2中。
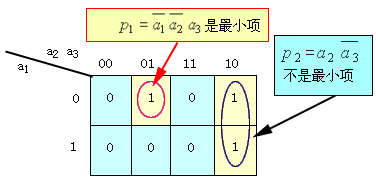
最小项在卡诺图(见图4.1)中对应于最小的方格。对应于一个小方格，因而它是最小项；而
对应于两个小方格，所以它不是最小项。
蕴涵项(implicant)
布尔函数f的"与-或"表达式中的每一乘积项都叫作f的蕴涵项。例如：
中的乘积项
和
都是函数f的蕴涵项。
质蕴涵项(Prime
lmplicant，PI)
设函数f有多个蕴涵项，若某个蕴涵项i所包含的最小项集合不是任何别的蕴涵项所包含的最小项集合的子集的话，则称i为函数f的质蕴涵项。图4.2中的质蕴涵项是覆盖着下列最小项的集合：2
- 3，3 - 7，4 - 5，5 - 7 - 13 - 15，8 - 10和2 - 10。13 - 15不是质蕴涵项，因为它是集合5 -
7 - 13 - 15的子集。
必要质蕴涵项(Essential Prime Implicant，EPI )
若某个最小项只被一个质蕴涵项所包含，则称此最小项为特征最小项，包含特征最小项的质蕴涵项为必要质蕴涵项，在布尔函数最小化的过程中，必要质蕴涵项是必须选取的。
图4．2中共有三个必要质蕴涵项：4 - 5(最小项4只被此质蕴涵项所覆盖)，8 - 10(最小项8只被此质蕴涵项所覆盖)，5 - 7 -
13 - 15 (最小项13和15只被此质蕴涵项所覆盖)。
|
图4．1 最小项在卡诺图中的表示 |
