有些竞争冒险可能使电路的工作状态产生永久性的后果,称为临界冒险。例如时钟信号中出现的尖峰脉冲可能使得触发器误触发,造成错误的后果。对于有反馈电路,因为产生的竞争冒险又可能反馈回输入端,也有可能使电路误动作。
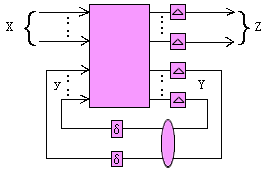
图3.18表示具有反馈电路的一种模型,设输入信号到达输出端z和y的延迟时间为D,每根反馈线上都有一个纯延迟元件,其延迟时间为d,并且D>>d。此外,设输入向量x的持续时间(包括值通过及X通过的持续时间)为t,假定D<< t, 那末,输入向量的任何变化都会引起反馈的变化,并引起对该元件的重新计算。如果新的输出值和上一次的输出值不相等,还会再次引起对该元件的计算,如此反复迭代计算,直到新的输出值和上一次的输出值相等, 即电路达到稳定状态为止。这时即可根据模拟结果波形判断其竞争冒险情况。
|
图3.18 反馈电路模型
 |
有反馈回路时的三值模拟算法如下:
//相邻两个稳态值向量分别为Xa与Xc,xb为过渡过程插入的向量,01或10跳变插入X,无跳变时插入相同的值:
即0X1, 1X0, 000, 111。
for 每个时钟周期
{
1. X通过:
取输入向量xb;
while (当前状态值未达到稳定 and 未达到最大迭代次数)
根据输入向量计算当前时间的状态值;//计算方法与一般逻辑模拟算法相同,循环计算直到稳定或达到最大次数为止。
if (当前状态未稳定)//未稳定而达到规定最大循环次数的情况
报告错误信息:"X通过过程中电路有振荡";
2.值通过:
取输入向量xc;
while (当前状态值未达到稳定 and 未达到最大迭代次数)
根据输入向量计算当前时间的状态值;//计算方法与一般逻辑模拟算法相同,循环计算直到稳定或达到最大次数为止。
if (当前状态未稳定)//未稳定而达到规定最大循环次数的情况
报告错误信息:"值通过过程中电路有振荡";
3.判断有无冒险,如果有冒险报告错误信息;
}