当一个逻辑门的几个输入端同时改变状态，并且其输出信号值依赖于输入信号跳变的次序，就有可能存在一个潜在的冒险(Hazard)。
　　图3.16说明二端与门产生冒险的原因。当其输入端分别为上跳或下跳时，理想状态其输出值保持为'0'。但由于参数分布性，上跳与下跳不可能绝对在同一时刻。若上跳先于下跳，则在瞬间出现两个输入端同时为'1'的情况。于是输出端在瞬间出现正尖峰脉冲；若下跳先于上跳，则不会出现尖峰脉冲。与此类似，当或门的一个输入端的下跳早于另一个输入端的上跳时，会出现负尖峰脉冲。
图3.16 与门的冒险
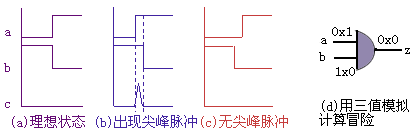　　三值模拟可以检测静态冒险，它增加一个值'X'来表示跳变过程中的瞬间信号值。为了检测静态冒险，要在所有输入波形中增加过渡态，即在所有的跳变过程中插入一个'X'。对于某一时刻不变化的信号，过渡值等于稳态值。模拟过程中，不但要对稳态值进行计算，而且要对插入的过渡态进行计算。当信号由'0'变'1'或'1'变'0'时，插入作为过渡态的'X'，将输入序列分别记为 "0X1"和 "1X0"（如图3.16d中的信号a和b所示）。由于'X'and 'X' = 'X'，故得输出序列"0X0"。表示在两个稳态中有可能出现'1'（序列"010"），也有可能保持'0'（序列"000"）。恰好反映了图3.16中(b)和(c)表示的两种情况。
　　上面的例子中出现的冒险称为静态冒险，是在信号值保持不变的过程中出现的毛刺。还有一种冒险是在动态变化过程中出现的，称为动态冒险，如图3.17所示。
图3.17 动态冒险
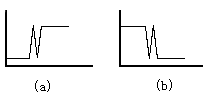　　三值模拟算法中，对每个模拟步，都要进行两次通过：第1步为Ｘ通过，用求输出过渡向量；第2步为值通过，求输出稳态向量。对于其中某一个信号，可以根据由两个稳态值与它们中间的过渡值组成的值的序列按下列方法判断是否存在冒险：对每个信号，若两个稳态值不等于'X'，而过渡值等于'X'，则该信号有静态冒险；若第一个稳态值不等于 'X'，而过渡值与后面的稳态值都等于'X'，则该信号有动态冒险或者其取值不定。
　　例如，当某一信号的模拟结果的值序列中含有"1X1"或"0X0"，则表示该信号存在静态冒险。而当含有"1XX"或"0XX"时，则表示其存在动态冒险。其中两边的值为稳态值，即值通过过程中得到的值，而中间的值为过渡值，即X通过过程中得到的值。