假设神经元网络包含ν个可见单元，即可与外界发生联系的单元。而是所需要的训练模型，它们只表现在这ν个可见单元的输出端上。对训练系统来说，不仅要规定这些所需的状态，同时要规定它们出现的概率。因而训练的目的是控制网络状态的能量级，使得网络在自由运行的条件下，各种状态发生的概率与它们在训练时一致。
　　为了说明Hinton等提出的训练方法，设各个状态所期望的概率表示为
　　
　　而当网络在自由运行时，各种状态出现的概率可写为
　　
　　因此训练的目的是使为此Hinton等人提出一种衡量这两组概率差异的函数
　　　　　(6-34)
　　显然当时，该G值为零。上式中第一项则起到加权的作用。训练的目的是使G值减小到零。
　　Hinton等人提出了一个很重要的方法，即
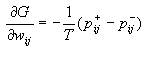　　　　　(6-35)
　　其中是结点间的联系权值，T是Boltzmann意义上的温度，与是指第i与j结点同时处于激励状态的概率，是训练中要求的概率，则是网络自由运行时出现的概率。
　　Hinton等人提出的这种方法具有十分重要的价值。首先他们找到一种使G值降低的训练方法。为使G值降低而调整联接权值只需知道，与其它结点的信息无关。因此只要按与有关的两结点的上述值成正比的值调整即可，该比值则需经实验确定。其次这种训练方法对可见结点与隐结点是一视同仁的，因而解决了隐结点参数训练的问题。
　　上述训练方法可归纳如下：
　　1.训练过程的目的是调整包含隐结点在内所有结点的联接权值；
　　2.将所见结点的状态一个接一个地按其所需概率锁定在所需状态上；
　　3.在这种锁定过程中计算每个所联接两端同时处于激励状态的概率并存储下来；
　　4.让网络自由运行，对每个记录其两端同时处于激励状态的概率；
　　5.对3与4所得结果进行比较，并因而调整其相应权值，使这两者越来越接近。
　　至于算法的细节，读者可参阅有关文章与书籍。