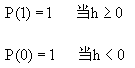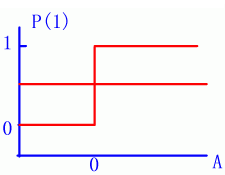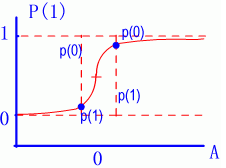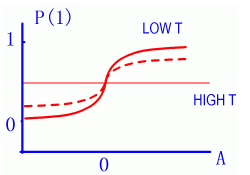
6.3.2 在Hopfield模型中引入不确定性 　　如果将Hopfield模型中处于激励状态的结点的状态用“1”表示，而处于抑制状态则用“0”表示。则根据Hopfield模型结点中所使用的激励函数性质，结点的状态与其激励值h有确定的关系。如果概率函数P(1)与P(0)分别表示结点状态与激励值h的关系，则有 　　　　　(6-31) 并可用图6-5中的(a)表示。 图6-5 活概率函数 　　在引入“噪声”概念之后，结点的状态则具有一定的随机性，因此对应某一个激励值h，p(0)与p(1)不再只限于0或1两种可能性，而呈现出两者各占某种比例的状态。当然随着h值的增大，p(1)的比例应增高，反之p(0)的比例要增大。所期望的情况如图6-5(b)所示。 　　a.阈值函数 　　b.boltzmann激活概率函数 　　c.温度对激活概率函数的影响 　　这样一来，网络结点的状态就具有了不确定性。为了对这种不确定性加以控制，Hinton等提出以下计算P(1)的公式 　　　　　(6-32) 　　其中h为结点的激励值，而T是一种控制参数，就像温度对分子随机运动的影响一样，因而也被称为“温度”。该函数可用图6-6的形式表示。显然对不同的温度时同一h值P(1)有不同值。而Hopfield模型对应于T=0的情况。 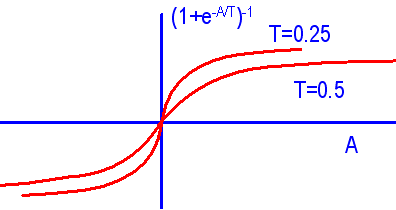图6-6 S-形Boltzmann激活概率函数 　　显然引入了这种不确定性后，网络从某种状态转换到另一状态会与Hopfield模型中不同。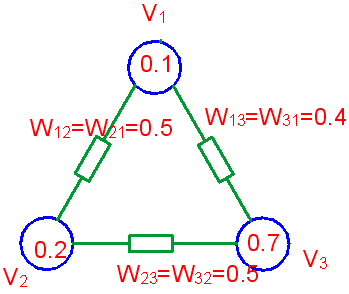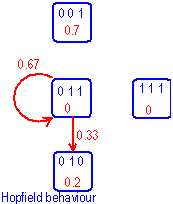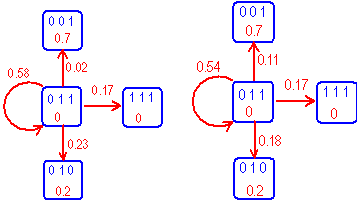例如有一个三结点的网络，其相应的参数为： 图6-7 不同温度下状态转移概率 　　如果分别按Hopfield模型与T＝0.25时的Boltzmann机两种方式计算该网络从某种状态转换成另一种状态的可能性，各种转换发生的可能性就会不同。图6-7中表示的就是该网络下在011状态时，针对两种不同模型，其状态变化的可能性。在异步工作状态下，如果每一时刻只有一个结点能参与状态的变化，因此在本例中每个结点只有1/3的可能性参与这种事件，而其实际改变状态的可能性又与其现状态及相应的p(1)与p(0)值有关，因而第j个结点改变其状态的可能性为 　　　　　(6-33) 　　其中是该结点的现状态，与是其当前激励值计算的状态概率。按Hopfitld模型工作，保留011状态的可能性是0.67，转移到010状态的可能性为0.33。而按T=0.25的Boltzmann机工作，则从011状态转移至010的概率为0.23，并出现了向001转移的可能性。其它转移可能性见图6-7。而010则是其一个稳态。按Hopfield模型方式，一旦网络进入该状态，它就没有可能再发生状态转移。而对Boltxmann机来说，它还可以0.15，0.15及0.13的可能性分别转移到011，000与110这三种状态去。如果某种稳态是我们所不期望的寄生稳态，那么这种转移可能性对逃逸这种稳态是有用的。此外在Boltzmann模型工作方式中，网络从某一状态转移到另一状态的可能性与这两种状态对应的能量函数值有关。如果从能量高的状态转移到能量值低的状态，且两者能量值差值大，则发生这种转移的可能性也大。反之，如从能量低转移到能量高就在太容易了。因此应设法使寄生稳态处于能量函数值相对较高的状态，从而使从这些状态中转移出去的可能性增大。这需要在训练过程中解决。