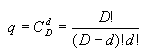前面已提到特征选择在这里的含意是指，由原有D维特征所组成的特征空间中选出若干个特征，组成描述样本的新特征空间，即从原有的D维空间选取一个d维子空间(d＜D)，在该子空间中进行模式识别。为此有两个问题要解决，一个是选择特性的标准，也就是选择前面讨论过的可分离性判据，以这些判据为准则，使所选择的d维子空间具有最大的可分离性。这个问题在前述章节中已讨论过，这里不再具体讨论。另一个问题是要找出较好的特征选择方法，以在允许的时间内选择出一组最优的特征。所谓最优的特征组，就是要找到合适的特征的组合。如果从逐个特征配组进行性能比较的话，即穷举的算法，特征配组的数量可能极大，组合配置的数目按下式计算 |
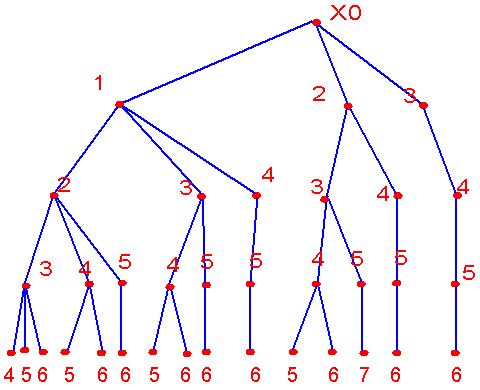 图 4.5 |
| 图4.5的搜索树形结构表示搜索过程，根结点为原特征空间，包含全部特征，在这里是六个特征。除了根结点外，其它结点每删除一个特征，结点上的号表示被删特征序号。叶结点本身也删除一个特征，而剩下的特征组的特征数为d，在此为2。叶结点的个数由不同的d个特征配置的个数决定。由于每个结点只删除一个结点，因而从根结点到叶结点所在的层数由D-d决定，在此为4层(不算根结点所在的第零层)。该树的结构有一特点，即每一层结点的直接后继结点数各不相同，但是却有规律性。譬如第一层中三个结点各自的直接后继结点数从左到右分别是3、2与1个，而第一层的最左结点的三个直接后继结点的后继结点数也是如此。那末这样一种树结构是根据什么原理设计的呢? 该种方法的基本原理是，先找到一个d维特征组合，期望该特征组合的判据值尽可能大，以此为界值。然后将该界值与后继搜索到的结点判据值比较。如该结点的判据值已小于此界值，则由于判据的单调性，该结点及其子树上的所有结点不需要再搜索，其下属结点也就没有可能是最优解。如果当前计算结点的判据值(除叶结点外)大于此界值，则搜索直至其下属叶结点。如发现叶结点的判据值大于界值时，界值被该判据值更新。这种原理体现在该树的搜索过程中，搜索至第一个叶结点d，其判据值取代初始界值，然后回溯至e点，如e点相应特征组的判据值大于界值，搜索将沿f→g方向进行，否则将立即回溯至O点，界值更改只可能发生在叶结点。 |
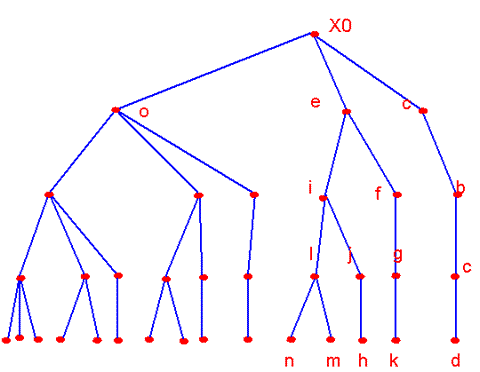 图 4.6 |
| 实际上整个树结构是在搜索过程中展开的。在每个当前计算结点要执行的计算按是否处于回溯过程而不同。如处在非回溯过程，则执行以下几个计算： (1)确定直接后继结点数，以根结点为例。在该结点上共有六个特征  。该结点层数为i＝0，因此到达其下属某一叶结点(图4.6的d点)需经(D-d-i)层(此处为4)，因而需有相应数目的特征备删除用，并且只有r-(D-d-i)个特征可用作另外的回溯支路入口，因而一结点的直接后继点数 
(4-78)在根结点处r＝6，故q＝3，有三个直接后继结点。 (2) 确定直接后继结点要删除的特征 为了使每一当前计算结点尽可能早地接触到判据值较大的叶结点，在确定直接后继点待删除特征时，先计算现有ψ中删去其中一特征的相应判据值  ，并将相应的特征Xj按判据值由小到大的顺序分别赋予相应直接后继结点，图4.5中第一层的三个结点的待删除特征分别为 与 ，也就是说有 
显然如此安排含有这样一种假设，即认为删除对分类较有效的特征，会使判据值有明显减小。 为了说明以上两步我们再举a点为例，此时a点的  为
,所以 ，无分支结点。在d点， ,
达到叶结点，剩下特征组为 。至于回溯过程中要执行的任务是将第i层的ψ加上第i-1层被删除的特征，并检查其分支路数q，待发现到  时，就到达回溯转折点，转入其相邻左边第i层结点。如图4.6中从最右端首先回溯至根结点，由根结点转至e点，此时 再转入非回溯阶段。以上讨论了“分支定界”的最优搜索算法。该算法避免了部分d个特征组合的判据计算，与穷举相比节约了时间。但是由于在搜索过程中要计算中间的判据值，因此在d很小或d很接近D时，还不如使用穷举法。另外该算法必须使用具有单调性的判据。有时在理论上具有单调性的判据，在实际运用样本计算时，可能不再具备单调性，特别当各类分布密度是用非参数法估计时，很可能发生这种情况，因此存在不能保证结果为最优的可能性。 |
，以及基于概率距离的判据JD,JC,JB都满足上述关系。