本章前述部分着重讨论了基于各种原理与判据的特征提取方法。从其工作原理来看可以分成两大类。一类基于对样本在特征空间分布的距离度量。其基本思想是通过原有特征向量线性组合而成新的特征向量，做到既降维，又能尽可能体现类间分离，类内聚集的原则。在欧氏距离度量的条件下所提出的几种判据都是从这一点出发的，如
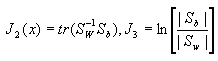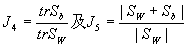　　,,等。其中描述类内离散度与类间离散度的矩阵与是两个主要描述样本分布的数据。利用K-L变换进行特征提取的几个方法也是出于同样的原理。它是在原特征空间进行的一种特殊的正交变换，在其产生矩阵确定的范围内消除了特征各分量间的相关性，并从中选择有关的特征子空间。这一类方法由于直接从样本之间在特征空间中的距离度量出发，具有直观与计算简便等优点。但由于没有从概率分布考虑，与计算错误率没有直接的关系，当不同类别的样本存在交迭区时，所采用的特征提取结果无法保证有较小的错误率。
　　另一大类则是从概率分布的差异出发，制订出反映概率分布差异的判据，以此确定特征如何提取。这类判据由于与错误率之间可能存在单调或上界关系等，因此从错误率角度考虑有一定的合理性。但是使用这种方法需要有概率分布的知识，并且只是在概率分布具有简单形式时，计算才比较简便。熵概念的运用是描述概率分布另一种有用的形式，使用时也可仿造本章中所举例子，将一些量折算成概率形式，利用熵原理构造的判据，进行特征提取。
　　特征提取各个方法中都有一个共同的特点，即判别函数的极值往往演变为找有关距阵的特征值与特征向量，由相应的特征向量组成坐标系统的基向量。计算有关矩阵的特征值矩阵与特征向量，选择前d个大特征值，以它们相应的特征向量构成坐标系统，这是大部特征提取方法的基本做法。这一点与下面讨论的特征选择方法是不相同的。
　　在特征提取方法中所使用的各种判据原理不尽相同。从以上讨论可以看出，一般希望判据能满足以下几点要求：
　　(1) 与错误概率或其上界或下界有单调关系，如能做到这一点，当判据达到其最大值时，一般说来其错误概率较小。前面提到的基于概率分布的判据，如Bhattacharyya距离和Chernoff界限符合这个条件，而基于特征空间分布欧氏距离度量的一些判据与错误概率没有直接关系。
　　(2) 判据在特征独立时有可加性，即
　　
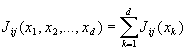
这里用 表示第i与j类之间的可分性准则函数， 表示相应的k分量的可分性准则函数。
　　(3) 可分性判别应满足

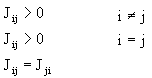
即有可分性，及对称性。
　　(4) 单调性，是指维数增多时，判据值不应减少。