此节不作基本要求
　　从上面所讨论的方法看出，为了兼顾类内离散度与类间离散度，包含在类均值向量内的分类信息并没有全部利用。换句话说，类平均向量的判别信息在K-L坐标系的各个分量中都有反映，并没有得到最优压缩。就拿图4.3的例子来说，如仅从类均值向量所包含的分类判别信息全部被利用这一点出发，应选择包含这两均值向量连线方向在内的坐标系。但是简单地从类均值向量来确定特征子空间，虽然实现很容易，但一般不能满足各分量间互不相关的要求。
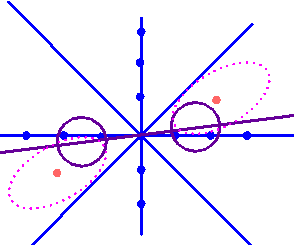　　有一种特殊的例外情况，这种情况是，如果类内离散度矩阵是一个单位矩阵，即它在特征空间中以超球体分布，就可做到既保持各分量的不相关性，同时又能充分利用包含在类均值向量内的差别信息。从这种特殊情况得到启发，一种充分利用类均值向量所包含的判别信息的方法因此而产生。具体说来这种方法分成两步。

图 4.4
　　第一步： 先用原坐标系中作为产生矩阵，实行K-L变换，将原有数据的相关性消除掉。所得到的K-L坐标系中的新，是一个对角矩阵，其相应的K-L坐标系为U，由原特征值对应的特征向量组成。然后进一步实行变换，使该矩阵变为单位矩阵。从原到单位矩阵I的变换为B，有
 　　　(4-74)
　　其中　　(4-75)
　　U为的特征向量矩阵，∧为特征值矩阵。
　　经过B变换后的类间离散矩阵应有
　　　　(4-76)
　　第二步，以作为产生矩阵，作第二次K-L变换，由于 的秩最多是c-1，所以最多只有c-1个非零特征值。设共有d个非零特征值，d≤c-1，则该d个非零特征值就可表示类均值向量所包含的全部信息。设这d个特征向量系统用V'表示，即
 (4-77)
　　从而整个变换W为
　　
　　例 4.3 数据同上例，求保持类均值向量中全部分类信
息条件下压缩为一维特征空间的坐标轴。
　　今有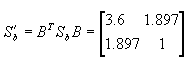
　　

　　的特征值矩阵是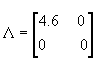

　　与非零的特征值对应的特征向量是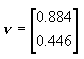

　　所以
　　图4.4给出了两次变换步骤以及变换对数据产生的作用。由图中看出，样本原为椭圆形分布，经白化处理后转化为圆形分布，此时为单位矩阵。均值向量也随之变化，最后得到的均值向量作为降维后的一维坐标。
　　这种方法主要用在类别数C比原D维特征向量的维数D小得多的情况，由于的秩最多为C-1，因此可使特征维数降至C维以下。