此节不作基本要求
上面讨论K-L变换时得出K-L坐标系是由 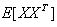 的特征值对应的特征向量产生,因而 的特征值对应的特征向量产生,因而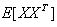 被称为K-L坐标系的产生矩阵。实际上使用不同的向量作为产生矩阵,会得到不同的K-L坐标系,从而满足不同的分类要求。例如可用样本数据的协方差矩阵 被称为K-L坐标系的产生矩阵。实际上使用不同的向量作为产生矩阵,会得到不同的K-L坐标系,从而满足不同的分类要求。例如可用样本数据的协方差矩阵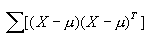 作为产生矩阵。这跟 作为产生矩阵。这跟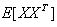 所产生的K-L坐标系是一样的。另一种按分类均值 所产生的K-L坐标系是一样的。另一种按分类均值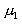 及各类先验概率 及各类先验概率 考虑。如各类别协方差矩阵为 考虑。如各类别协方差矩阵为 则可以用类内离散矩阵SW作为产生矩阵, 则可以用类内离散矩阵SW作为产生矩阵,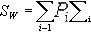 其效果相当于只按类内离散程度进行特征选取。如果只以某一样本集的协方差矩阵
其效果相当于只按类内离散程度进行特征选取。如果只以某一样本集的协方差矩阵 作为产生矩阵,则效果是对该类样本集有信息压缩的最优性质。 作为产生矩阵,则效果是对该类样本集有信息压缩的最优性质。
下面讨论一些不同的使用K-L变换的方法。
4.6.3.1
利用类均值向量提取特征
此节不作基本要求
在讨论欧氏距离度量进行特征提取时,曾提到一些判据是从使类内尽可能密集,类间尽可能分开的设计思想出发的,可见类内离散程度与类间离散程度要结合起来考虑。如何在K-L变换方法中体现对这两者的兼顾可用不同的做法。一种做法是先按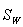 ,即类内离散度矩阵提供的信息(作为产生矩阵)产生相应的K-L坐标系统,从而把包含在原向量中各分量的相关性消除,并得到在新坐标系中各分量离散的程度。然后对均值向量在这些坐标中分离的程度作出判断,决定在各坐标轴分量均值向量所能提供的相对可分性信息。为此可设判据为: ,即类内离散度矩阵提供的信息(作为产生矩阵)产生相应的K-L坐标系统,从而把包含在原向量中各分量的相关性消除,并得到在新坐标系中各分量离散的程度。然后对均值向量在这些坐标中分离的程度作出判断,决定在各坐标轴分量均值向量所能提供的相对可分性信息。为此可设判据为:
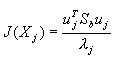 (4-72) (4-72)
其中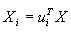 表示在新坐标轴ui上的分量,
表示在新坐标轴ui上的分量,
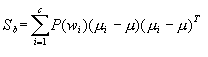
是类间离散度矩阵,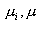 分别是类均值与总体均值.
分别是类均值与总体均值. 是各类先验概率。实际上(4-72)也可写作
是各类先验概率。实际上(4-72)也可写作
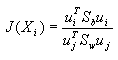 (4-73) (4-73)
可见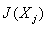 是类间离散度与类内离散度在uj这坐标的分量之比
是类间离散度与类内离散度在uj这坐标的分量之比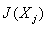 越大,表明在新坐标系中该坐标抽包含较多可分性信息。因此为了降低特征空间的维数,可以将各分量按 越大,表明在新坐标系中该坐标抽包含较多可分性信息。因此为了降低特征空间的维数,可以将各分量按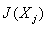 大小重新排列,使 大小重新排列,使

并取与前面d个最大的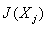 值相对应的特征向量uj,j=1,...,d作为特征空间的基向量。 值相对应的特征向量uj,j=1,...,d作为特征空间的基向量。
例4.2 设有两类问题,其先验概率相等,即 ,样本均值向量分别为:
,样本均值向量分别为:
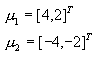
协方差矩阵分别是
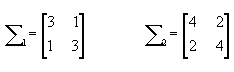
为了把维数从2压缩为1,求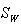 的特征向量 的特征向量
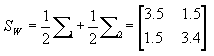
它的特征值矩阵和特征向量分别是:

今有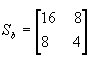
可计算得
因此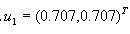 作为一维特征空间的坐标轴,见图4.3。 作为一维特征空间的坐标轴,见图4.3。
|