从下面“用KL变换作人脸合成”的例子中可以看出,每个分量都承担着各自不同的作用,也就是说各个分量之间的关系是不怎么关联的。为了说明这点我们有必要进一步了解K-L变换的性质,这就是1,训练集样本的不同系数ci与cj之间是不相关的。以及2,训练是样本集在使用K-L变换的正交基描述后,它的协方差矩阵成为对角矩阵。它们的数学证明见讲义。并注意图4-2用一个二维空间分布的数据说明K-L变换的性质。
K-L变换具有一些很重要的性质,因而在特征提取中很有用。
(1) 样本的K-L变换系数ci与cj是无关的,这可从样本集中任两个系数的乘积的期望值看出
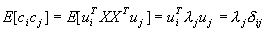 (4-69) (4-69)
其中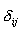 为Kronecker符号,即 为Kronecker符号,即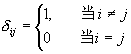 。
。
(4-69)式表明不同系数是无关的,同时还表明相同系数的方差就是ψ矩阵的相应特征值。特征值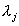 大,则表明样本沿该坐标轴uj分量的方差大,分布分散。 大,则表明样本沿该坐标轴uj分量的方差大,分布分散。
(2) K-L变换后的协方差矩阵为对角矩阵。
如我们令在K-L变换后的D维坐标系统中样本向量为X',则
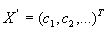
而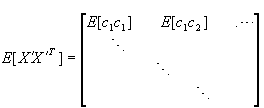
将(4-69)代入得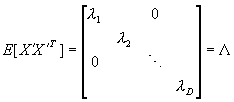 (4-71)
(4-71)
∧为一对角矩阵,或写成 ,其中U为由(u1,...uD)组成的向量矩阵。这表明经过K-L变换后,原向量各分量之间存在的相关性已被消除。图4.2表示了一个二维空间中椭圆分布的样本集,在用K-L变换后新的坐标系中各分量的相关性消除。而在原坐标中x1,x2两个分量之间存在很明显的相关性。图4.2还反映了样本的u1分量比较分散,因而对分类可能起较大作用,而u2则对分类无太大作用,可以去掉。
,其中U为由(u1,...uD)组成的向量矩阵。这表明经过K-L变换后,原向量各分量之间存在的相关性已被消除。图4.2表示了一个二维空间中椭圆分布的样本集,在用K-L变换后新的坐标系中各分量的相关性消除。而在原坐标中x1,x2两个分量之间存在很明显的相关性。图4.2还反映了样本的u1分量比较分散,因而对分类可能起较大作用,而u2则对分类无太大作用,可以去掉。
|
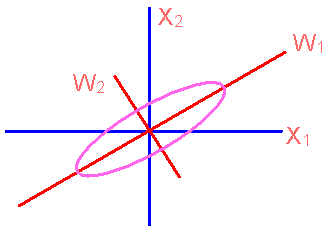
图 4.2 |
K-L变换的一些典型应用
上面我们从数学的角度分析了K-L变换的性质。归结起来,它消除了各分量之间的相关性,因而用它来描述事物时,可以减少描述量的冗余性,做到用最经济有效的方法描述事物。下面结合一些应用实例来说明如何运用K-L变换的这一性质。
1.降维与压缩
以人脸图象这个例子看,K-L变换的降维效果是十分明显的。对一幅人脸图象,如果它由M行与N到象素组成,则原始的特征空间维数就应为M×N。而如果在K-L变换以及只用到30个基,那么维数就降至30,由此可见降维的效果是极其明显的。另一方面降维与数据压缩又是紧密联系在一起的。譬如原训练样本集的数量为V,而现采用30个基,每个基实质上是一幅图象,再加上每幅图象的描述参数(式(补4-3)中的C),数据量是大大降低,尤其是图象数很大时,压缩量是十分明显的。
2.构造参数模型
使用K-L变换不仅仅起到降维与压缩数据的作用,更重要的是每个描述量都有明确的意义,因而改变某一个参数就可让图象按所需要的方向变化。在没有使用K-L变换的原数据集中对图象的描述量是每个象素的灰度值,而弧立地改变某个象素的灰度值是没有意义的。而在使用K-L变换后,每个描述量都有其各自的作用。因此通过改变这些参数的值就可实现对模型的有效描述,这在图象生成中是很有用的。因此利用K-L变换构造出可控制的,连续可调的参数模型在人脸识别与人脸图象重构采方面的应用是十分有效的。
3.人脸识别
利用K-L变换进行人脸图象识别是一个著名的方法。其原理十分简单,首先搜集要识别的人的人脸图象,建立人脸图象库,然后利用K-L变换确定相应的人脸基图象,再反过来用这些基图象对人脸图象库中的有人脸图象进行K-L变换,从而得到每幅图象的参数向量(试问用哪个公式?)并将每幅图的参数向量存起来。在识别时,先对一张所输入的脸图象进行必要的规范化,再进行K-L变换分析,得到其参数向量。将这个参数向量与库中每幅图的参数向量进行比较,找到最相似的参数向量,也就等于找到最相似的人脸,从而认为所输入的人脸图象就是库内该人的一张人脸,
完成了识别过程。
(试问:这种识别方法属于哪一种方法?)
4.人脸图象合成
用K-L变换构造参数模型的另一种典型用途是人脸图象合成。从下面的例子中可以看出,有目的的控制各个分量的比例,也就是通过调整参数向量。可以将一幅不带表情图象改变成带各种表情的图象,称为人脸表情图象合成。下图为生成各种表情图象的示例。 |
 |
图中从上到下分别对应KL变换后第一至第四个主分量,这四个主分量代表了人在不同表情下面部图像的主要变化。使用这四个分量,就可以描述面部表情的大部分变化,与变换以前的描述方法对比,原来要用几万个分量(图像中的各个象素)来描述这种情感图像的变化。
从左到右是对每个分量赋以不同的值,而得到的合成图像,其中中间一列是取均值时的对应结果,最左一列是取到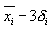 (均值减三倍标准方差)时的合成图像,同样的,按照图像上边一行标出的意义,可以合成其它几列表情图像。 (均值减三倍标准方差)时的合成图像,同样的,按照图像上边一行标出的意义,可以合成其它几列表情图像。 |