现在我们讨论第二个问题，即K-L变换的最佳是指什么含义，在这里我们讨论的是特征空间的降维，因此这个最佳是与降维联系起来的。对我们降维来说，原特征空间是D维的，现希望降至d维d<D。不失一般性，可以认为D为无限大的情况，并设原信号可用一组正交为换基ui表示，见(4-59)。现要求降维至d维，也就是说将d+1维以上的成分略去，显然原信号会因此受到一些损失，我们将其表示成(4-60)形式，而每个信号的损失则表示成X与
之差。现在的问题是对我们讨论的问题，即给定一个训练样本集条件下要找一个好的正交变换，能使这种误差从总体上来说是最小。注意这里讲的是总体，这是因为降维以后，训练样本集中的每个样本数据都受到损失，要衡量的是总体效果。在这种情况下最常用的指标是均方误差最小，或称均方误差的期望值最小，这就是(4-61)式。这就是说要找的正交变换能使一组样本集的截均方误差的期望值为最小。K-L变换是一种正交变换，即将一个向量X，在某一种坐标系统中的描述，转换成用另一种基向量组成的坐标系表示。这组基向量是正交的，其中每个坐标基向量用ui表示，j=1,…,∞，因此，一个向量X可表示成
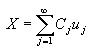(4-59)对一向量或一向量空间进行正交变换，可采用多种不同的正交坐标系，关键在于使用正交变换要达到的目的，不同的要求使用不同的正交变换。这里要讨论的是，如果我们将由(4-59)表示的无限多维基向量坐标系统改成有限维坐标系近似，即
(4-60)表示X的近似值或估计量，我们希望在同样维数条件下，使向量X的估计量误差最小。确切地说是使所引起的均方误差
(4-61)为最小。K-L变换可以实现这个目的。
要找满足(4-61)式为最小是一个求极值的问题，求最佳的是正交变换的基ui，i=1,…∞。因此还要满足变换是正交归一这个条件，因此这是一个求条件极值的问题，一般方法是利用拉格朗日乘子法将条件数值转换成一个求无条件极值的问题，观察从(4-61)到(4-69)的过程而(4-62)则是对拉格朗日函数g(ui)求偏导而得出的结果。
至于对某一个数据X的相应cj值，可以通过X与每一个基uj的点积来计算。由于不同的基之间是相互正交的，这个点积值就是cj的值，即cj=ujTx(补4-2)如不明白可看讲义中的(4-65)与(4-66)如果我们要求一组系数cj，并将其表示成一个向量形式C=(c1,c2,……)T，则我们可以从(补4-2)得：
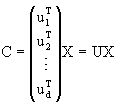(补4-3)则U就是一个变换矩阵，其中每一行是某一个正交基向量的转置。由X计算C称为对X的分解。反过来，如果我们希望用C重构信号X，则根据(被4-1)，它是各个成分之和。如果我们将对应于每个基ui的成分表示成xi，则重构的信号又可表示成一个向量形式。
则
(补4-4)显然，与原向量X是有差别的，是原向量的一个近似，要使
与X的差异越小，则要用更多维数的正交基。如果将
代入(4-61)可得到
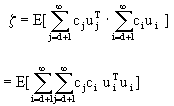
由于uj,j＝1,…，∞是正交归一坐标系，有
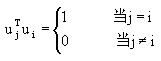(4-63)所以有
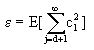(4-64)系数cj可以利用正交坐标系的特性得到。如令某一基向量uj与向量X作点积，则有
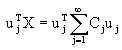(4-65)利用(4-63)有
(4-66)代入(4-64)得
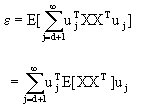(4-67)如令
，则有
欲使该均方误差ε为最小，就变成在确保正交变换的条件下，使ε达最小的问题，这可用拉格朗日乘子法求解。为此设一函数
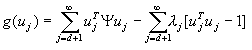
并令其对uj求导数，得
(4-68)可见向量
应是
矩阵的特征值
的特征向量，而此时截断误差为
。如将按其大小顺序排列，即
则取前d项特征值对应的特征向量组成的坐标系，可使向量的均方误差为最小。
满足上述条件的变换就是K-L变换。
在结束4.6.1节的学习时，我们还要强调K-L变换的特殊性。K-L变换是一种独特的正交变换，它与一些常用的正交变换不同。最常见的正交谈 换如富里叶变换，哈达玛变换离散余弦变换等都是一种通用的正交变换，它们各自有固定的形式，如富里叶变换的基是以频率为参数的e的括数函数族组成。它主要用来对数据作频谱分析。滤波等。而K-L变换的基并没有固定的形式，它是从对给定数据等{x}进行计算产生的。换句话说，给定的数据集不同，得到的K-L变换基函数也因此而不同。正是因为它对给定数据集{x}存在依赖关系，它能在降低维数时仍能较好地描述数据，因此是模式识别中降低特征空间维数的有效方法。但是由于它的正交基函数族是从训练样本集中计算出来的，因此并不存在一种对任何数据都适用的K-L变换基，一般的作法是先用一组训练数据计算出K-L变换基，然没用这组基来重构或分析其它数据。面举一个在人脸表情分析的例子，使我们增加对K-L变换的感性认识。
例：
为了实现对人脸表情进行分析，或生成对不同表情的人脸，可以使用K-L变换。具体做法是，先获取一组带不同表情的人脸图象作为训练样本集，例如补图4-1是其中的一个日本女孩子做六种不同典型表情时的图象。如果我们将训练样本集表示成{x}，则图4-1中的每一幅图就是一个数据x，利用这些数据计算出相应的协方差矩阵4。然后对这个矩阵进行特征值分解，求得相应的特征向量。我们把特征值按其数值进行降序排列，并选出前 项用来重构人脸不同的表情图象，为了说明。