4.6.1 Karhunen-Loeve变换 　　正交变换概念 　　变换是一种工具，它的用途归根结底是用来描述事物，特别是描述信号用的。例如我们看到一个复杂的时序信号，我们希望能够对它进行描述，特别是希望用一些经济有效的方式进行描述。描述事物的基本方法之一是将复杂的事物化成简单事物的组合, 或对其进行分解，分析其组成的成分。例如看一波形，我们希望知道它是快速变化的(高频)，还是缓慢变化的(低频)，或是一成不变的(常量)。如它既有快正变化的成分，又有缓慢变化的成分，又有常量部分，那么我们往往希望将它的成分析取出来。这时候我们就要用到变换。变换的实质是一套度量用的工具，例如用大尺子度量大的东西，用小尺子度量小的东西，在信号处理中用高频，低频或常量来衡量一个信号中的各种不同成分。对某一套完整的工具就称为某种变换，如富里叶变换就是用一套随时间正弦、余弦信号作为度量工具，这些正弦，余弦信号的频率是各不相同的，才能度量出信号中相应的不同频率成分。例如，补图4-1中的信号只有一个单一频率的简谐信号，而补图4-2(a)中信号就不是一个简谐波号所描述的，它起码可以分解成补图4-2中的两个成分，一是基波，另一是三次谐波。 补图 4-1 补图 4-2(a) 补图 4-2(b) 　　由此可以看出，对事物可以有不同的描述方法，如补图4-2(a)是对信号的一种描述，而补图4-2(b)则利用成分分解，得到该事物的另一种描述。当将一事物从一种描述转换成另一种描述时，就要用不同的工具，因而每一套工具称为一种变换。 　　为了对复杂事物进行经济有效的描述，我们希望将其分解成相互独立的成分，譬如我们分析其快速变化的成分时，就希望它只不再混杂其它成分。用富里叶变换为例，希望它分析出某种频率的成分，就不要包含其它任何频率的成分。这就要求，作为变换的工具中的每个成分是相互独立的，用其中某一个工具就只能从信号中分析出一种成分，而分析不出其它成分。 　　用变换对信号进行分析，所使用的数学工具是点积。点积的实质就是两个信号中相同成分之间乘积之总和，补图4-3中列举了一些点积运算的例补图4-3(a)中是两个随时间连续变化的信号，它们之间的点积运算定义为 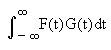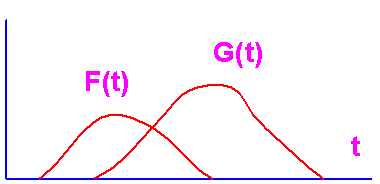补图 4-3 (a) 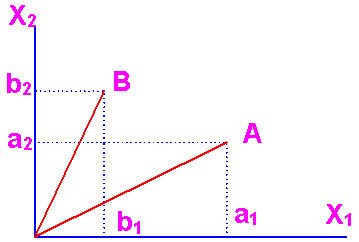补图 4-3 (b) 　　在这里同一成分是指同一时刻t两个信号的值F(t)与G(t)。积分就是在整个时间域上求和。而补图4-3(b)中的向量A与B在一个二维空间定义，它们两者分别含有成分为(a1,a2)与(b1，b2),a1与b1是两者的同一种成分，a2与b2则是另一种成分。故它们的点积定义为a1b1+a2b2，在这种条件下就不需要积分，而只是简单求和。 　　点积运算的结果是一个数值，或大于零，小于零或等于零，等于零的情况在补图4-3(b)中出现在A与B之间夹角为90°的情况，这表明B中没有A的成分，A中也没有B的成分，因此又称相互正交。由此我们知道作为一种变换，如果这种变换中的每一种成分与其它成分都正交时，它们之间的关系就相互独立了，每一种成分的作用是其它成分所不能代替的。拿富里叶变换来说，频率为f的成分只能靠变换频率为f的成分去析取。另一方面也说明了这套变换必须是完备的，也就是它必须包含一切必要的成分，例如必须有基波的任何一次整数信频率的谐波，否则就会对信号分析不全面。 　　综合以上分析，我们可以将对这种变换的定义归为： 　　如果将这种变换中的每一成分，同一个向量ui表示，i是其下标，原理上可以到∞，则我们要求的正交变换可表示成： 　　 　　这里ui与uj的点积采用了矩阵乘积的形式，此时其中一个向量要表示成转置形式，上式中要求uiTuj=1，是考虑到ui是作为度量事物的单位应用的，它本身的模应该为1，ui又称为某一个基。而被分解后的任何事物(在此指信号)可等成各种成分之和。故任一信号X可等成 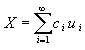(被4-1)其中ci是相应基ui的相应成分。