从这里开始到例4.1之前这一段可略去不看。 　　需要指出的是，尽管对不同的判据，具有相同的变换形式，但是这些判据的具体使用仍是不同的。这一点可从J5的进一步分析中看出： (4-15)式表示J5采用(Sw+Sb)及Sw的行列式之比值。由于Sw都是对称矩阵，则通过相似变换可变成对角矩阵。前面已经指出J2，J3与J5在D维空间经非退化线性变换其值不变，因此我们可以通过将J5表示式中的分子，分母都变成对角矩阵来分析，并且希望有 　　　　　　　(4-20) 　　及 (4-21) 　　其中U为相似变换中用的变换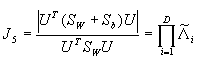，为一对角矩阵，而I是单位矩阵。在这种情况下(4-15)式可写成 　　　　　　(4-22) 　　其中是对角矩阵主对角线上的元素。那末满足(4-20)与(4-21)式的变换U是什么样的D×D矩阵呢？ 　　如果(4-21)成立，则可写成其逆矩阵形式，有 　　　　　　(4-23) 　　将(4-23)与(4-20)结合有 　　(4-24) 　　(4-25) 　　可见是矩阵的特征值矩阵。从(4-25)式还可看出如果用∧表示 的特征值矩阵，则 　　 　　因此若用λi表示∧的主对角线各特征，则 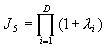　　(4-26) 　　与(4-19)相比，可以看出由大特征值对应的特征向量组成的变换矩阵可使J2与J5这两判据都达最大值。J5与J2不同处在于，在处理多类问题时，不致于选取那些只对两类有很好可分性而对其余各类效果不大的特征。而对J2来说，只要有一个λi很大就会发生这种情况。 　　至于J3与J1的优点是计算方便，不需要存储任何矩阵。 　　例4.1给出一个数量的例子，并且说明在两类别情况下，由于Sb的秩只可能为1，因此优化以后的降维特征空间只是一个一维的特征空间，该特征空间实质上就是对应于Fisher准则求得的线性分类器法向量。如果讨论的是多类别问题，则优化后的维数至多为类别数减1。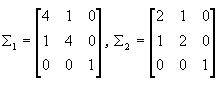 　　例4.1给定先验概率相等的两类，其均值向量分别为：和，协方差矩阵是： 　　 　　求用J2判据的最优特征提取。 　　解： 根据前面的分析，应先求，再求此矩的特征矩阵。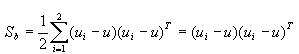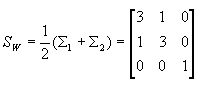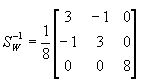 　　今有混合均值 　　类间离散度矩阵： 　　类内离散度矩阵 　　则 　　接着，需求的特征值矩阵。由于这是一个两类别问题，总均值向量μ值是两个均值向量μ1和μ2的线性求和，则中只有一个是独立的，因此的秩是一，换句话说只有一个非零特征值，W是D×1矩阵，是一个向量W，求该向量需解 　　而代入式得 　　 　　由于是一个标量，所以 　　 　　因此利用W向量对原始的两维样本进行线性变换，得到新的一维分布，特征空间从两维降到一维，并满足J2判据。