其中W是一个D×d维矩阵,现在的问题是要利用判据找出一种线性变换,利用这种变换,实现这种判据的极值化。例如使上一节定义的判据J2(x)达到极值。
这一节的思路是这样的:首先说明J2(x)等这些判据在不降维的线性变换条件下是不能体现优化的,然而说明如何找到使判据优化的降维线性变换。在不降维条件下,因为变换前的
由于J2(x)左式括弧中的矩阵与J2'(x)式右项括弧中的矩阵是相似关系,也就是说S
而由于矩阵的迹是所有特征值之和(见4-19),因此J2(x)=J2'(x)判据值不会改变。这就是说,对于任何一个不降维的线性变换(W是D×D矩阵)J2判据的值都是一样的。另一个结论是在降维条件下,即使用任何一个非奇异线性变换矩阵(D×d)进行降维,则所得
前面已说明特征提取在这里的意义是指对原始的D维特征空间进行一个降维的变换,从而使用维数减少后的特征空间。因此特征提取在这里意味着找到一个变换W,对原始特征向量
W为D×d矩阵,并希望变换后的特征向量能满足使某个准则函数达到极值的要求。在这一节中讨论按欧氏距离度量的准则,它们列举在上一小节中。
值得注意的是上面列出的准则中,如果对特征空间实行一个D×D矩阵的非奇异线性变换,J2,J3与 都保持不变。例如若对原特征空间实行一D×D线性变换A,则离散度矩阵Sb与SW变为Sb=ASbAT及SW=ASWAT,而映射变换后的J2(X)有:
因而以下讨论的特征提取变换,只考虑是降维的,即用D×d矩阵(d<D)进行变换。其目的是在维数d的条件下,使相应的判据为最大。
在使用J2判据的情况下,可以将J=判据表示成变换W的函数,有
(4-17)
求使J2(W)最大的W解可利用特征值方法。前面曾提到如果W是一个D×D的线性变换,则J2是不变的,而此时(4-17)可进一步表示成
(4-18)
其中用WD代替(4-17)中的W,以强调是D×D变换。如果 是 的各特征值对应的特征向量所组成的矩阵,则由(4-18)式可得:
(4-19)
其中λi表示 的各特征值。(4-19)式表明D维特征空间中,J2判据的值是 矩阵的全部特征值之和。那么由对应于d个最大的特征值的特征向量所组成的矩阵W(D×d),就能使所得到的d维特征满足J2判据最大的要求。
虽然J2,J3,J5乃至J4所采用的计算方法各不相同,但都得到一个同样的结论,如果矩阵 的特征值λ1,λ=,…λD按大小顺序列为:
λ1≥λ2≥λ3≥…≥λD
则选择前d个特征值所对应的特征向量组成变换矩阵W,都可使这些判据达到最大值。
基于距离可分性判据的特征优化过程是通过一个线性变换实现的。设在原特征空间一个样本向量表示成Y(D维)而在优化以及的特征空间中,样本向量表示成X(d维)而X与Y之间的关系是:
其中W是一个D×d维矩阵,现在的问题是要利用判据找出一种线性变换,利用这种变换,实现这种判据的极值化。例如使上一节定义的判据J2(x)达到极值。
这一节的思路是这样的:首先说明J2(x)等这些判据在不降维的线性变换条件下是不能体现优化的,然而说明如何找到使判据优化的降维线性变换。在不降维条件下,因为变换前的 ,则变换后的离散矩阵 而 因此有
(4-18)
由于J2(x)左式括弧中的矩阵与J2′(x)式右项括弧中的矩阵是相似关系,也就是说S 与 是相似关系,因此它们的特征值都是一样的。
而由于矩阵的迹是所有特征值之和(见4-19),因此J2(x)=J2’(x)判据值不会改变。这就是说,对于任何一个不降维的线性变换(W是D×D矩阵)J2判据的值都是一样的。另一个结论是在降维条件下,即使用任何一个非奇异线性变换矩阵(D×d)进行降维,则所得 的迹也必然小于原 的迹。经过推导可以证明,只要对 作特征值分解,并将特征值按降序排列,则取前d项特征值对应的特征向量构成的线性变换矩阵W,能使降维后的特征空间使J2(x)判据值为最大。
前面已说明特征提取在这里的意义是指对原始的D维特征空间进行一个降维的变换,从而使用维数减少后的特征空间。因此特征提取在这里意味着找到一个变换W,对原始特征向量Y=[y1,…,yD]T实行映射变换W: Y→X,得到维数减少的向量X=[x=,…,xd]T,即
X=WTY (4-16)
W为D×d矩阵,并希望变换后的特征向量能满足使某个准则函数达到极值的要求。在这一节中讨论按欧氏距离度量的准则,它们列举在上一小节中。
值得注意的是上面列出的准则中,如果对特征空间实行一个D×D矩阵的非奇异线性变换,J2,J3与 都保持不变。例如若对原特征空间实行一D×D线性变换A,则离散度矩阵

因而以下讨论的特征提取变换,只考虑是降维的,即用D×d矩阵(d<D)进行变换。其目的是在维数d的条件下,使相应的判据为最大。
在使用J2判据的情况下,可以将J=判据表示成变换W的函数,有
求使J2(W)最大的W解可利用特征值方法。前面曾提到如果W是一个D×D的线性变换,则J2是不变的,而此时(4-17)可进一步表示成
其中用WD代替(4-17)中的W,以强调是D×D变换。如果
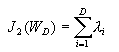 (4-19)
(4-19)其中λi表示
虽然J2,J3,J5乃至J4所采用的计算方法各不相同,但都得到一个同样的结论,如果矩阵
则选择前d个特征值所对应的特征向量组成变换矩阵W,都可使这些判据达到最大值。