为了度量类内、类间的距离,也可用另一种描述方法,即描述样本的离散程度的方法。在讨论Fisher准则时曾用过两个描述离散度的矩阵。一个是类间离散矩阵Sb,按(3-18)有
另一个是类内离散度矩阵SW,按(3-16)与(3-17)有:
SW=S1+S2
及
以上式子是针对两类别情况的,如果推广至c类别情况,同时考虑各类的先验概率Pi不等,则可将上列各式表示成:
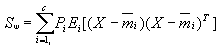 (4-4)
(4-4)其中
利用(4-3)与(4-4)式可以将基于距离的可分性判据表示成以下形式:
1 计算特征向量间平均距离的判据
其中“tr”表示矩阵的迹。(4-5)式实际上是从计算特征向量间总平均距离的公式推导得到的,该式可写成
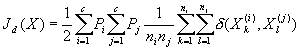 (4-6)
(4-6)其中Pi、Pj分别表示各类的先验概率,ni、nj分别是第i与j类的样本个数,
利用均值向量
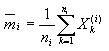 (4-8)
(4-8)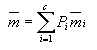 (4-9)
(4-9)代入(4-6)式可得
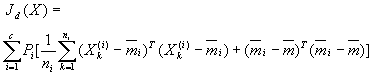 (4-10)
(4-10)(4-10)中右边括弧里的前一项涉及类内各特征向量之间的平方距离,后一项则是类间距离项。后一项可写成
显然利用(4-10)与(4-11)就可得到(4-5)。需指出的是由(4-6)推导的各式是利用有限样本数据,因此得到的都是母体各量的估计值,而(4-5)式用的是母体的离散度矩阵。
2 考虑类内类间欧氏距离的其它判据
判据Jd(X)是计算特征向量的总平均距离,以下一些判据则基于使类间离散度尽量大,类内离散度尽量小的考虑而提出:
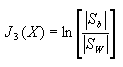 (4-13)
(4-13)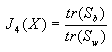 (4-14)
(4-14)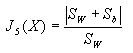 (4-15)
(4-15)其中